Širdies ir kraujagyslių ligos yra viena pagrindinių mirties priežasčių pasaulyje. Viena iš šių ligų yra susijusi su prieširdžių virpėjimu. Sveiko žmogaus širdis plaka reguliariai, tačiau atsiradus prieširdžių virpėjimui ritmingas širdies darbas sutrinka. Tuomet ypač svarbų vaidmenį atlieka kairysis prieširdis, o tiksliau – jo dalis, vadinama apendiksu. Dėl prieširdžių virpėjimo, kai kraujas apendikse užsistovi, gali susidaryti trombas ir žmogų gali ištikti insultas. Todėl šiuo metu Vilniaus universiteto Taikomosios matematikos institute suburta mokslininkų – matematikos, informatikos ir kardiochirurgijos specialistų komanda kuria matematinį modelį, kuris padėtų įvertinti trombo formavimosi greitį.
Širdies darbas ir matematika
Žmogaus kūne kraujagyslės suformuoja labai sudėtingos geometrijos tinklą. Jis sudarytas iš stambių kraujagyslių (arterijų, venų), kurios pereina į smulkesnes (arterioles, venules), o šios galiausiai išsišakoja į mažyčius kapiliarus, leidžiančius išnešioti kraują po visus audinius, aprūpinti juos deguonimi ir surinkti šalutinius produktus, tokius kaip anglies dvideginis. Visą šį kraujo judėjimą užtikrina nenuilstantis širdies darbas.
Pats kraujas yra kompleksiškos prigimties skystis. Jis sudarytas iš plazmos, daugybės ląstelių (baltųjų ir raudonųjų kraujo kūnelių) ir už kraujo krešėjimą atsakingų trombocitų. Tekant kraujui, stambesni raudonieji kraujo kūneliai, dar vadinami eritrocitais, išstumia daug mažesnius ir lengvesnius trombocitus kraujagyslių sienelių link. Šis ląstelių elgesys yra labai svarbus modeliuojant žmogaus kūno fiziologiją, o kraujo tekėjimo modeliavimas yra itin sudėtingas procesas.
Šiuo metu skaičiavimams taikomas paprasčiausias matematinis modelis siejamas su Navjė ir Stokso lygtimis (Navier–Stokes equations), kurios aprašo klampaus nespūdaus skysčio tekėjimą. 2000 m. buvo paskelbtos septynios pagrindinės naujojo tūkstantmečio matematikos problemos (Millennium Prize Problems). Už kiekvieną šių problemų sprendimą skiriama vieno milijono JAV dolerių premija. Iki šių dienų yra išspręsta tik viena iš septynių tūkstantmečio problemų.
Nestacionariosios Navjė ir Stokso lygčių sistemos išsprendžiamumas, jos sprendinių glodumas ir vienatis taip pat yra viena iš septynių tūkstantmečio problemų. Tai parodo Navjė ir Stokso lygčių tematikos svarbą ir aktualumą. Realistiniu trimačiu atveju kompiuterinis kraujo tekėjimo modeliavimas, susijęs su Navjė ir Stokso lygčių taikymais, yra vis dar neįveikiama problema, kadangi tam reikia milžiniškų skaičiavimo išteklių. Pasaulyje vykdoma daug mokslinių tyrimų, kurių tikslas – sumažinti šiuos išteklius.
Skaičiavimo išteklių mažinimas
Norint kuo tiksliau atspindėti realybę, Navjė ir Stokso lygtys turi būti tiriamos sudėtingos geometrijos srityse, atitinkančiose kraujagyslių tinklus. Tačiau realių kraujagyslių tinklų tankumas ir komplikuota geometrija neleidžia Navjė ir Stokso lygčių sistemos ištirti žinomais trimačiais skaitiniais metodais, o su dabartinėmis skaičiavimo technologijomis prieinami vienmačiai metodai duoda rezultatus, kurių tikslumas yra per mažas naudoti chirurginių procedūrų metu.
Todėl vykdant projektą „Klampaus tekėjimo sudėtingos geometrijos srityse daugiaskaliai modeliai“ buvo pasiūlytas ir matematiškai pagrįstas metodas, kuris sujungia vienmačius kraujagyslių modelius su trimačiais „priartinimais“ (angl. zooms) mažose kraujagyslių išsišakojimų, krešulių ar kitų sužalojimų zonose (1 pav.).
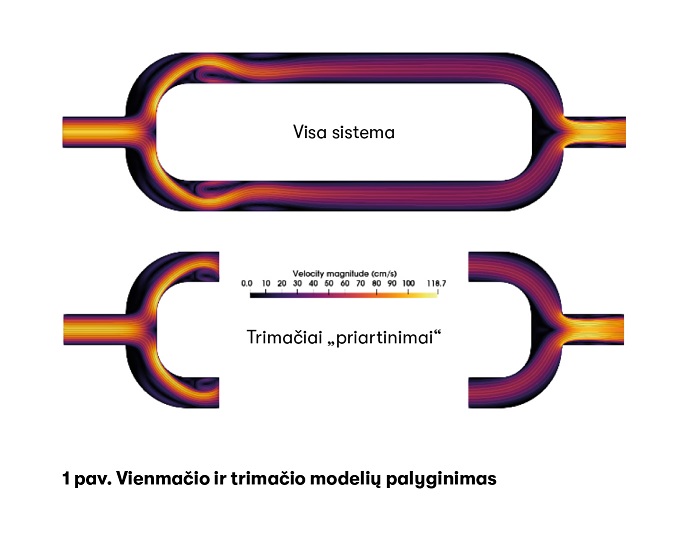
Pagrindinis iššūkis – nustatyti ir matematiškai pagrįsti, kurioje vietoje netoli išsišakojimo ar krešulio reikia pereiti iš vienmačio modeliavimo į trimatį tokiu būdu, kad išliktų pakankamas skaičiavimų tikslumas. Be to, vienmačio ir trimačio modelių sandūroje buvo sukonstruotos ir matematiškai pagrįstos tinkamos sujungimo sąlygos.
Šis naujas įrankis smarkiai sumažina kompiuterinio skaičiavimo išteklius ir pagreitina skaičiavimus.
Matematikos taikymai gydant širdies ir kraujagyslių ligas
Tarpdisciplininis projektas „Daugiaskalis matematinis ir kompiuterinis srautų modeliavimas tinkluose: taikymai širdies ir kraujagyslių ligų gydymui“, siejantis taikomąją matematiką ir mediciną, yra skirtas širdies ir kraujagyslių ligų tyrimui.
Mokslininkų tikslas – sukurti ir plėtoti naujus matematinius metodus bei kompiuterinius įrankius, kurie leistų širdies ir kraujagyslių ligų patologijas pirmiausia sumodeliuoti kompiuterio ekrane ir tik paskui atlikti chirurgines intervencijas.
Mokslinių tyrimų metu ypatingas dėmesys skiriamas kairiojo prieširdžio apendikso geometrijos modeliavimui. Šie tyrimai gali padėti spręsti trombo formavimosi kairiajame prieširdyje problemą. Trombo susidarymas kairiojo prieširdžio apendikse susijęs su širdies ritmo sutrikimais (prieširdžių virpėjimu). Kairiojo prieširdžio apendikso geometrija yra labai įvairi: ji gali būti panaši į viščiuko sparnelį, kaktusą, žiedinį kopūstą, vėjarodį ir kt.
Priklausomai nuo šios geometrijos, tam tikrose apendikso vietose užsistovėjus kraujui gana greitai (kartais per kelias valandas) gali susidaryti trombai. Stagnacijos zonų trombocitų aktyvavimo mechanizmas iki šiol nėra gerai žinomas.
Šio projekto metu kuriamas matematinis modelis, kuris padėtų įvertinti trombo formavimosi greitį, atsižvelgiant į kairiojo prieširdžio apendikso geometriją. Norint atlikti kompiuterinius skaičiavimus, pirmiausia reikia gauti konkretaus paciento kairiojo prieširdžio apendikso kompiuterinės tomografijos duomenis. Tiriant kompiuteriniu tomografu kairiojo prieširdžio apendiksas skenuojamas plonais sluoksniais ir gaunami dvimačiai jo skerspjūvių vaizdai. Tuomet iš dvimačių vaizdų sudaroma trimatė kairiojo prieširdžio apendikso geometrija (2 pav.). Kai ši geometrija yra tinkamo kompiuteriniams skaičiavimams formato, atliekami skaitiniai eksperimentai.
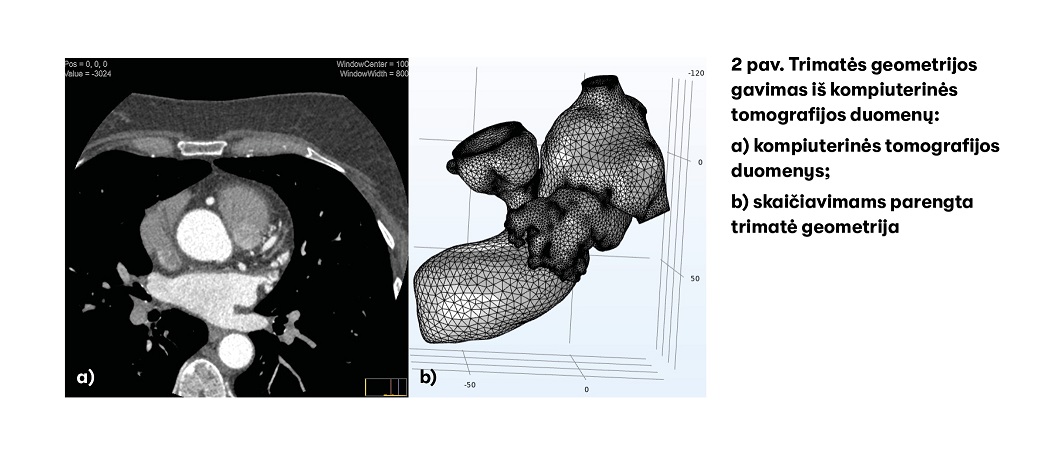
Galutinius tyrimo rezultatus, kaip papildomą informaciją prieš operaciją, galės interpretuoti ir naudoti gydytojai.
Šio projekto sėkmė neįmanoma be glaudaus matematikų ir medikų bendradarbiavimo. O kaip sakė filosofas Immanuelis Kantas, „kiekviename gamtos moksle esama tiek tiesos, kiek esama matematikos“.
Prof. habil. dr. Grigory Panasenko,
prof. habil. dr. Konstantinas Pileckas,
doc. dr. Kristina Kaulakytė
„Spectrum“
