Autorius prof. Rimas Norvaiša
 Birželio 18-20 dienomis Vilniuje viešėjo lenkų matematikas Zbigniew Marciniak. Lietuvos matematikų draugijos 60-oje konferencijoje jis skaitė pranešimą „Pokyčių vėjai matematikos mokyme“. Prieš pasidalindamas keletu jo minčių iš pranešimo, remdamasis keliais Z. Marciniak gyvenimo faktais, noriu paaiškinti šio įrašo pavadinimą.
Birželio 18-20 dienomis Vilniuje viešėjo lenkų matematikas Zbigniew Marciniak. Lietuvos matematikų draugijos 60-oje konferencijoje jis skaitė pranešimą „Pokyčių vėjai matematikos mokyme“. Prieš pasidalindamas keletu jo minčių iš pranešimo, remdamasis keliais Z. Marciniak gyvenimo faktais, noriu paaiškinti šio įrašo pavadinimą.
Matematikos ambasadorius visuomenėje
Baigęs Varšuvos universitetą 1976 metais prof. Z. Marciniak jame dirba iki šiol. Pagrindinis profesoriaus užsiėmimas – matematikos tyrimai grupių teorijos srityje. Disertaciją apgynė Amerikoje 1982 metais. Po to, nenorėdamas, kaip jis sakė, su vaikais šeimoje kalbėti angliškai, atsisakė puikaus pasiūlymo dirbti Kanadoje ir grįžo į Lenkiją, kur 1997 m. apgynė habilitacinį darbą. Už indėlį – remiant matematikai gabius vaikus – Z. Marciniak buvo suteikti šie apdovanojimai: „Silver Cross of Merit“ ir „The Knight’s Cross of the Order of Polonia Restituta“.
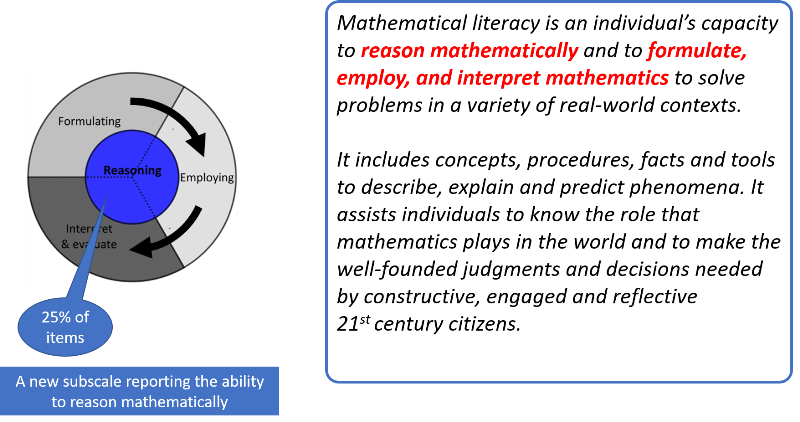
Nuo 2000 m. Z. Marciniak įsitraukė į matematikos mokymo problemų sprendimo veiklą tapdamas „Programme for International Student Assessment” (PISA) matematikos ekspertų grupės nariu. Jo iniciatyvumas ir veikla šioje grupėje paskatino Ekonominio bendradarbiavimo ir plėtros organizaciją (EBPO) pakeisti matematinio raštingumo sampratą suteikiant matematiniam samprotavimui didžiausią svarbą. Šios ekspertų grupės svarbus veiklos rezultatas yra matematinio samprotavimo vaidmens sureikšminimas ateinančiame PISA 2021 tyrime.
Nuo 2007 iki 2009 m. Z. Marciniak buvo paskirtas švietimo vice-ministru. Kadencijos metu rūpinosi ugdymo programos reformos principų kūrimu ir mokymo kokybe. Reformos rezultatus iliustruoja lenkų mokinių pasiekimai PISA 2012 tyrime. Juos pristatysiu vėliau. Šiuo metu Z. Marciniak yra prezidentas institucijos, kurios pavadinimo neversiu: „National Council for Science and Higher Education Poland“. Lenkijos valdžios struktūroje ši institucija yra ministerijos lygmens.
Pokyčių vėjai matematikos mokyme
Grįžtu prie Z. Marciniak pranešimo „Pokyčių vėjai matematikos mokyme“. Jis pradeda nuo šiandienos pasaulio iššūkių apžvalgos ir daro išvadą švietimui:

Švietimo sistema turi parengti mokinius taip, kad jie gebėtų spręsti nestandartines problemas, atpažinti melą ir įveikti jį. Kaip to pasiekti? Z. Marciniak nuomone, to pasiekti įmanoma mokant(is) matematikos.
Šiame kelyje svarbi tinkama matematikos mokymo(si) motyvacija:
 Netinkamos motyvacijos pavyzdžiai: kantriai praktikuokis
Netinkamos motyvacijos pavyzdžiai: kantriai praktikuokis

ir vėliau pamatysi kodėl tai turi prasmę...

Kitas prasto motyvavimo pavyzdys:
 Blogiausi motyvavimo pavyzdžiai – „matematikos nauda kasdieniniame gyvenime“:
Blogiausi motyvavimo pavyzdžiai – „matematikos nauda kasdieniniame gyvenime“:

Mokytis tas matematikos dalis, kurios yra naudingos gyvenime yra tas pats, kas skaityti tokią literatūrą, kuri yra naudinga gyvenime. Klausimas ko mokytis, o ką ignoruoti, tai klausimas kokias kultūros dalis ignoruoti?

Kiekvienai matematikos idėjai galima rasti jos reikšmingą vietą kultūros istorijoje. Pavyzdžiui, trikampių panašumo požymis antikos laikais leido Arystarchui įvertinti atstumą tarp Mėnulio ir Saulės:
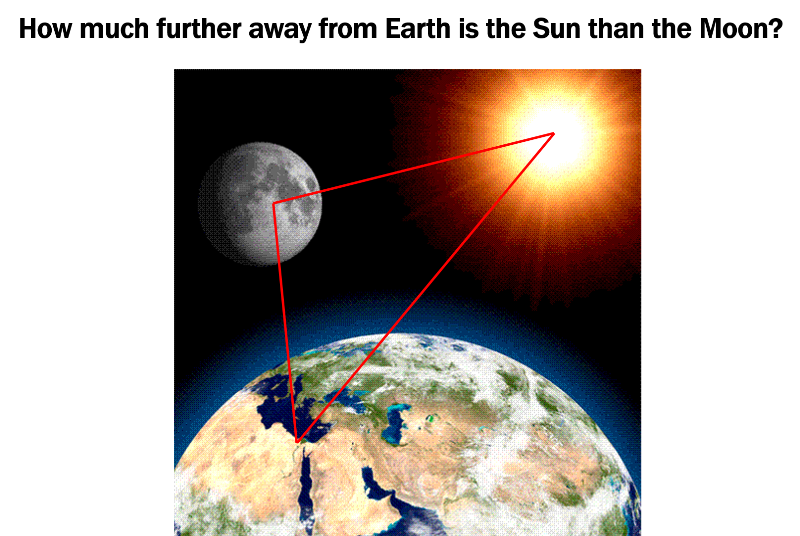
Susipažinti su matematikos idėjomis nepakanka. Reikia suprasti kaip tos idėjos veikia.
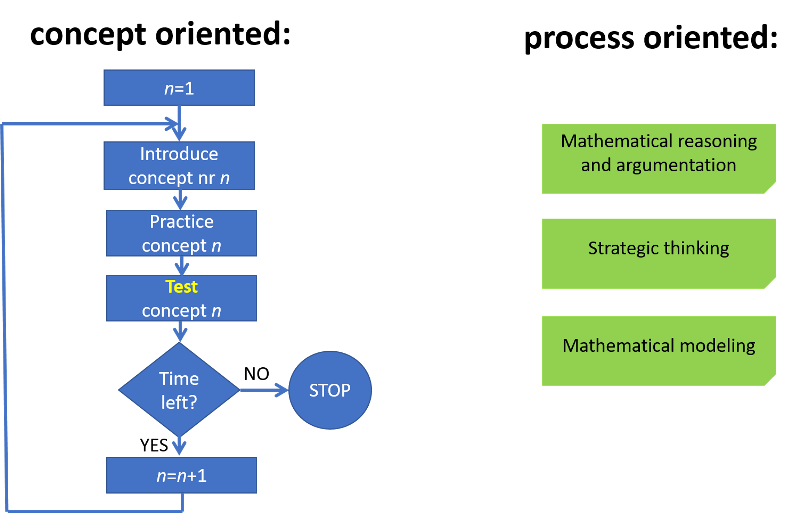
Toliau Z. Marciniak pateikė lenkų uždavinių iš 2014 m. brandos egzaminų pavyzdžių. Tipiška užduotis atrodo taip: įrodyti, kad...
Arba taip – apskaičiuoti šios figūros paviršiaus plotą:
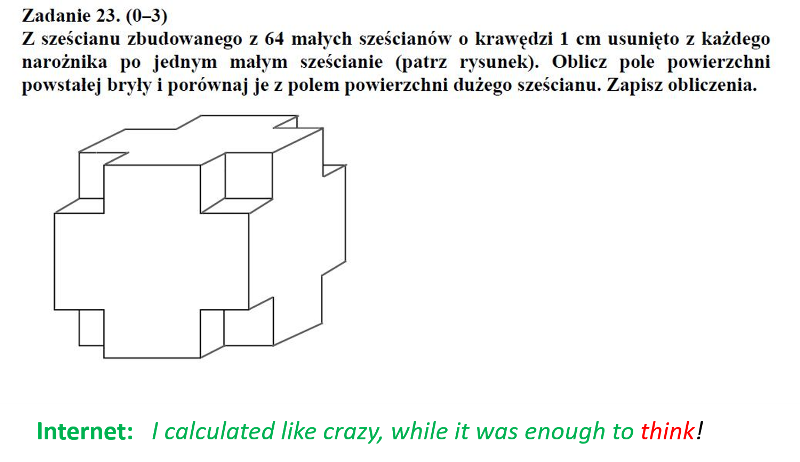 Tokio matematikos mokymo pasekmes iliustruoja PISA 2012 lenkų moksleivių pasiekimai. Primenu, kad matematikos mokymo turinio reforma vyko nuo 2008 metų.
Tokio matematikos mokymo pasekmes iliustruoja PISA 2012 lenkų moksleivių pasiekimai. Primenu, kad matematikos mokymo turinio reforma vyko nuo 2008 metų.
Taip pat primenu, kad tarptautinio tyrimo PISA tiriamuoju objektu yra penkiolikmečiai mokiniai. Kas trejus metus yra tiriamas moksleivių matematinis ir gamtamokslinis raštingumas bei skaitymo gebėjimai. Pastaruoju metu tiriami ir kitos rūšies raštingumas bei gebėjimai. Lietuviai šiame tyrime dalyvauja nuo 2006 metų. Matematinio raštingumo tyrime mokiniams siūloma atsakyti į skirtingo sunkumo klausimus. Pagal tai gebėjimų skalė yra sudaryta iš šešių lygių, kuriuose pirmas lygmuo atitinka lengviausius klausimus ir šeštas lygmuo – sunkiausius klausimus. Pagal tai į kokio sunkumo klausimus atsako mokiniai, jie papuola į atitinkamą lygmenį. Silpniausi mokiniai yra tuose lygmenyse kairėje, kurie žemiau esančioje lentelėje pažymėti simboliais < 1 ir 1. Stipriausi mokiniai yra tuose lygmenyse dešinėje, kurie pažymėti skaičiais 5 ir 6.
Z. Marciniak parodė lenkų moksleivių matematinio raštingumo vertinimo rezultatus 2003, 2006, 2009 ir 2012 m. (pavaizduoti skirtinga spalva). Reikėtų atkreipti dėmesį į tai, kaip pasikeitė rezultatai 2012 m. po to, kai 2008-2010 m. Lenkijoje buvo vykdoma Marciniak vadovaujam mokyklinės matematikos turinio reforma.
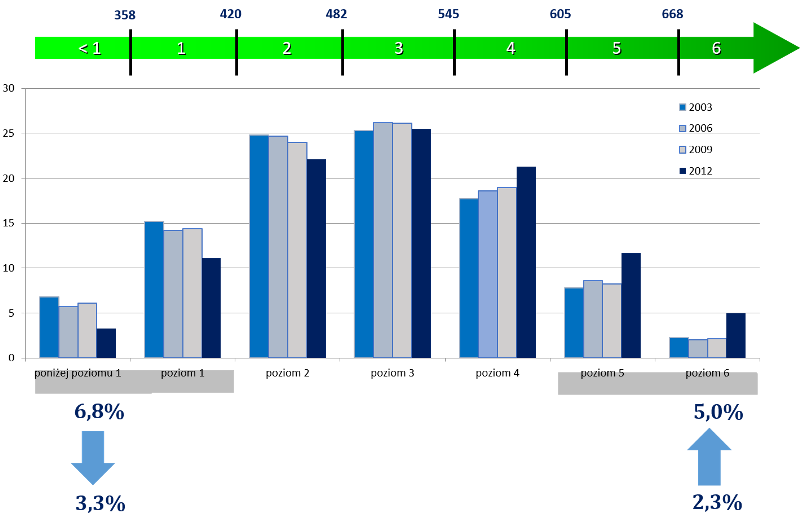
Ši lentelė rodo, kad 2012 metų tyrime <1 lygmens silpnų mokinių sumažėjo beveik dvigubai, nuo 6,8 proc. iki 3,3 proc. Tuo tarpu 6 lygmens stiprių mokinių padaugėjo beveik dvigubai, nuo 2,3 proc. iki 5 proc.
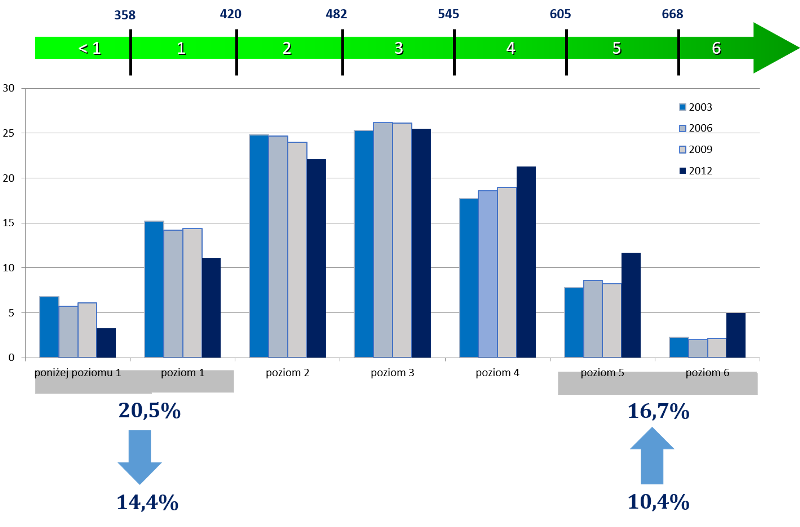
Šioje lentelėje matome, kad 2012 metų tyrime <1 arba 1 lygmens silpnų mokinių sumažėjo nuo 20,5 proc. iki 14,4 proc. Tuo tarpu 5 arba 6 lygmens stiprių mokinių padaugėjo nuo 10,4 proc. iki 16,7 proc.
Kitas etapas – PISA 2021. Šiame tyrime numatomi esminiai pokyčiai: matematinis samprotavimas yra matematinio raštingumo pagrindas, ketvirtis užduočių pagrįstos matematiniu samprotavimu ir susmulkinta mokinių pasiekimų skalė, norint įvertinti kaip samprotauja silpniausi vaikai. Taip pat įdomu kaip samprotauja tie, kurie buvo stipriausi pagal ankstesnius PISA uždavinius, pavyzdžiui suomiai?
Lenkų mokinių pasiekimai PISA 2012 tyrimuose pasaulyje sukėlė sensaciją. Bulgarai panoro sekti savo kaimynų lenkų pavyzdžiu bandydami taikyti jų reformos patirtį. Pasaulio bankas pradėjo skatinti kitas Europos Sąjungos šalis imti pavyzdį iš lenkų: Cross-Country Sharing of Poland’s Reform Experience: New Ideas for Education.
Kaip mokytis matematinio samprotavimo? Galima pradėti nuo loginių galvosūkių:

Spręsdami eilinį Sudoku galvosūkį, naudojame paprasčiausius matematinio samprotavimo būdus.
Tarp kitko, Z. Marciniak šeima leidžia galvosūkių žurnalą LOGI Danuta Marciniak.
Z. Marciniak pranešimo išvados:
- Matematika yra žymiai daugiau už įrankių dėžę.
- Į sąvokas orientuotas mokymas neatitinka dabarties iššūkių. Reikia mokyti matematinės galvosenos.
- Kaip ir iki šiol buvo, matematika pasiūlo geriausius atsakymus į dabarties problemas.
- Taip yra todėl, kad matematika yra viena iš geriausių žmonijos kultūros palikimo dalių.

Daugiau prof. Rimo Norvaišos straipsnių apie matematiką, mokslą ir švietimą galite rasti tinklaraštyje.
