A3 á idñ , čia A3 - lyginių keitinių grupė, turinti 3 elementus. A3 yra normalusis S3 pogrupis ir S3 ¤ A3 » Z3. Taigi, S3 yra išsprendžiama grupė.
Visos grupės, kurias mes nagrinėsime yra baigtinės. Kitoje paskaitoje mes matysime, kad polinomas yra išsprendžiamas tada ir tik tada, kada jo Galua grupė yra išsprendžiama. Tai ir yra pagrindinė šių grupių nagrinėjimo priežastis. Pradėsime apibrėžimu.
Apibrėžimas 8.1 Grupė G vadinama išsprendžiama, jeigu egzistuoja šios grupės tokia pogrupių grandinė G = N0 Ê N1 Ê Ê Nn , kai
(1) Ni yra normalusis Ni-1 pogrupis su visais i = 1,2,..., n,
(2) Ni-1 ¤ Ni yra ciklinės grupės su visais i = 1,2,...,n,
(3) Nn = á1ñ.
Šioje paskaitoje mes apsiribosime išsprendžiamų ir neišsprendžiamų grupių pavyzdžiais ir be įrodymų suformuluosime teiginius, aprašančius pakankamai dideles šių grupių klases.
Pavyzdys 8.2 Keitinių grupės S2 ir S3 yra išsprendžiamos.
Keitinių grupė S2 yra pati išsprendžiama, nes pati yra ciklinė.
Keitinių grupė S3 turi tokią pogrupių grandinę S3 A3 á idñ , čia A3 - lyginių keitinių grupė, turinti 3 elementus. A3 yra normalusis S3 pogrupis ir S3 ¤ A3 » Z3. Taigi, S3 yra išsprendžiama grupė.
Pavyzdys 8.3 Keitinių grupė S4 yra išsprendžiama.
Keitinių grupė S4 turi tokią pogrupių grandinę S4 A4 V á (13) (24)ñ á idñ , čia A4 - lyginių keitinių grupė, turinti 12 elementų; V - Kleino ketvirtinė grupė (Klein Viergruppe) : visi 2 -os eilės grupės A4 elementai ir id : V = {id,(12)(23), (13)(24), (14) (23)} » Z2 ´ Z2. Tai, kad A4 yra normalusis S4 pogrupis, V yra normalusis A4 pogrupis, á (13)(24)ñ yra normalusis V pogrupis paliekame įrodyti skaitytojui. Iš Lagranžo teoremos turime, kad |S4 ¤ A4| = 2, |A ¤ V | = 3, |V¤ á (13) (24)ñ | = 2, |á (13) (24)ñ ¤ á idñ | = 2, todėl S4 ¤ A4 » Z2, A ¤ V » Z3, V ¤ á (13) (24)ñ » Z2 ir á (13) (24)ñ ¤ á idñ i » Z2, t.y. visos faktorgrupės yra ciklinės. Gavome, kad S4 yra išsprendžiama.
Teorema 8.4 (Galua,1832) Keitinių grupė Sn , n ³ 5 yra neišsprendžiama.
Teoremos įrodymas remiasi lemomis.
Lema 8.5 Lyginių keitinių grupė An yra generuojama ilgio 3 ciklais.
Įrodymas. Bet kuris lyginis keitinys s yra lyginio skaičiaus transpozicijų sandauga: s = t1t2∙∙∙t2m-1t2m. Dviejų transpozicijų sandaugą visada galima užrašyti ilgio 3 ciklų sandauga:
|
(ij)(jl)=(ijl) | kai j=k |
|
|
| (ij)(kl)= | (ij)(jk)(jk)(kl)=(ijk)(jkl) | kai i;j;k;l skirtingi | ||
| Id | kai (ij)=(kl) |
Įrodyta.
Lema 8.6 Normalusis An (n ³ 5) pogrupis N, turintis ilgio 3 ciklą, sutampa su An
Įrodymas. Tegu c yra ilgio 3 ciklas pogrupyje N, o d yra bet kuris ilgio 3 ciklas grupėje An. Žinoma, kad egzistuoja toks s Î Sn, kad d = s s s -1. Jeigu s Î An, tai d Î N, nes N yra normalusis pogrupis. Jeigu s Ï An ir n ³ 5 , tai egzistuoja tokia transpozicija t Î Sn, kad ts Î An. Tada d = tdt-1 = ts cs -1t Î N ( t = t-1).
Įrodyta.
Lema 8.7 Kiekvienas An (n ³ 5) normalusis pogrupis N, N ¹ á idñ , turi ilgio 3 ciklą.
Įrodymas. Tegu s Î N ir s ¹ id. Jeigu s nėra ilgio 3 ciklas, tai mes parodysime kaip rasti tokį s ' Î N, s ' ¹ id, kuris nekeistų daugiau elementų iš {1,..., n} negu s (pastebėkime, kad ilgio 2 ciklas nėra lyginis keitinys ir todėl nepriklauso N ).
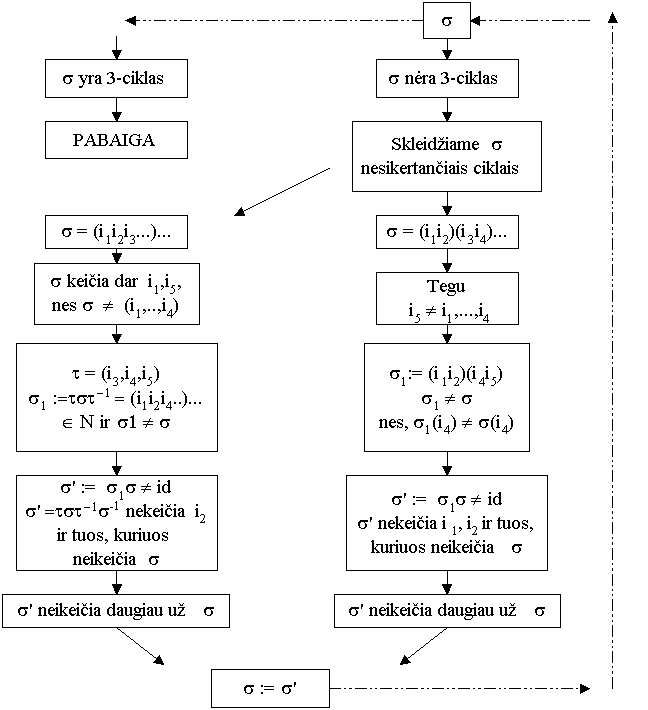
Įrodyta.
Iš šių trijų lemų mes turime, kad grupėje An (n ³ 5) nėra netrivialių normaliųjų pogrupių. Tokias grupes vadina paprastomis grupėmis. Taigi, An (n ³ 5) yra paprastoji grupė.
Lema 8.8 Keitinių grupėje Sn , n ³ 5 yra tik trys normalieji pogrupiai 1, An ir Sn.
Įrodymas. Tegu N yra normalusis Sn pogrupis. Tada NÇ An yra normalusis An pogrupis. Grupė An yra paprastoji, todėl arba NÇ An = An, arba NÇ An = á idñ . Pirmuoju atveju, N Ê An, o An indeksas grupėje yra 2, todėl N yra arba An, arba Sn. Antruoju atveju, funkcija j : N ® Sn /An , j (x) = xAn yra injektyvi ir todėl grupėje N yra arba 1, arba 2 elementai. Jeigu grupėje N yra 1 elementas, tai N = á idñ . Grupėje negali būti lygiai 2 elementų, nes jeigu c Î N, tai ir s cs -1 Î N su visiais s Î Sn.
Įrodyta.
Teoremos 8.4 įrodymas. Turime tik tokią keitinių grupės Sn normaliąją grandinę: S An á idñ . Bet grupė An yra nekomutatyvi: pvz.: (123)(124) = (14)(23), bet (124)(123) = (13)(24). Taigi, An yra neciklinė ir Sn nėra išsprendžiama.
Įrodyta.
Dabar pateiksime teoremas be įrodymų, aprašančias išsprendžiamų grupių klases.
Teorema 8.9 Visi išsprendžiamos grupės pogrupiai ir visos faktorgrupės yra išsprendžiamos grupės.
Teiginys 8.10 Baigtinė p -grupė G, t.y. grupė, turinti ps elementų, yra išsprendžiama.
Teiginys 8.11 Visos grupės, kurių eilė < 60; yra išsprendžiamos.
Teorema 8.12( Feit-Thomson,1963) Nelyginės eilės grupė yra išsprendžiama.