| Eilė | Komutatyvi grupė | Nekomutatyvi grupė |
| 2 | Z2 | - |
| 3 | Z3 | - |
| 4 | Z4 , Z2 x Z2 | - |
| 5 | Z5 | - |
| 6 | Z6 | S3 |
| 7 | Z7 | - |
| 8 | Z8 , Z4 x Z2 , Z2 x Z2 x Z2 | D4 , Q |
| 9 | Z9 , Z3 x Z3 | - |
| 10 | Z10 | D5 |
| 11 | Z11 | - |
| 12 | Z12 , Z6 x Z2 | A4 , D6 , Z3 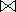 Z4 Z4 |
| 13 | Z13 | - |
| 14 | Z14 | D7 |
| 15 | Z15 | - |
Pradėkime nuo grupių, kurių eilė neviršija 15, lentelės.
| Eilė | Komutatyvi grupė | Nekomutatyvi grupė |
| 2 | Z2 | - |
| 3 | Z3 | - |
| 4 | Z4 , Z2 x Z2 | - |
| 5 | Z5 | - |
| 6 | Z6 | S3 |
| 7 | Z7 | - |
| 8 | Z8 , Z4 x Z2 , Z2 x Z2 x Z2 | D4 , Q |
| 9 | Z9 , Z3 x Z3 | - |
| 10 | Z10 | D5 |
| 11 | Z11 | - |
| 12 | Z12 , Z6 x Z2 | A4 , D6 , Z3 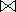 Z4 Z4 |
| 13 | Z13 | - |
| 14 | Z14 | D7 |
| 15 | Z15 | - |
Mums yra gerai pažįstamos Abelio grupės Zn. Tai ciklinės adicinės grupės generuotos elementu 1 : Zn = <1>. Kai n yra pirminis skaičius, tai egzistuoja tik viena n - osios eilės grupė - būtent Zn.
Parodysime, kad grupės, kurių eilė yra lygi p2, čia p - pirminis skaičius, yra Abelio grupės.
Grupės G elementas z vadinamas centriniu, jeigu zg = gz su visais g Î G. Visų grupės G centrinių elementų aibė Z ( G ) yra pogrupis, vadinamas grupės G centru. Viena iš svarbiausių centro savybių yra ta, kad grupės G, kurios eilė yra pm, čia p - pirminis, centras Z ( G ) yra netrivialus, t.y. jame yra nevienetiniai elementai.
Teiginys 4.1 Tegu G - nekomutatyvioji grupė. Tada faktorgrupė G / Z ( G ) ne ciklinė.
Įrodymas. Sakykime priešingai, G / Z ( G ) =
Įrodyta.
Teiginys 4.2 Grupė G, turinti p2 elementų, yra Abelio grupė.
Įrodymas. Minėjome, kad grupės G centras Z ( G ) yra netrivialus, todėl arba | Z ( G ) | = p, arba | Z ( G ) | = p2. Pirmuoju atveju faktorgrupė G / Z ( G ) yra p elementų ir todėl ji yra ciklinė grupė, antruoju atveju faktorgrupė G / Z ( G ) yra vienas elementas, t.y. grupė irgi yra ciklinė. Įrodymui baigti pakanka pasinaudoti Teiginiu 4.1.
Įrodyta.
Teorema 4.3 Tegu p - pirminis skaičius.
(1) Egzistuoja tik dvi neizomorfinės grupės, turinčios p2 elementų:
(2) Egzistuoja penkios grupės, turinčios p3 elementų: trys Abelio grupės
ir dvi nekomutatyvios grupės:
kaip p = 2, tai
kai p > 2, tai
Dabar apsistokime ties grupėmis, turinčiomis pq, čia p ir q - pirminiai, elemantais. Pasinaudosime klasikine L. Silovo teorema.
Teorema 4.4 ( Silov ) Tegu G - baigtinė grupė, kurios eilė |G| dalijasi iš pn ir nesidalija iš pn+1, čia p - pirminis.
(1) Su kiekvienu r ≤ n egzistuoja grupės G pogrupis, kurio eilė yra pr.
(2) Pogrupių, kurių eilė yra pn ( šie pogrupiai vadinami Silovo p - pogrupiais ), skaičius lygsta 1(mod p) ir dalija |G|.
Nagrinėkime grupę G, kurios eilė |G| = pq, čia p ir q - pirminiai ir p < q. Silovo p - ir q - grupės G pogrupiai, t.y. pogrupiai, kurių eilės yra p ir q, yra cikliniai. Tegu (a) ir (b) yra šie Silovo pogrupiai: |(a)| = p ir |(b)| = q. Iš Silovo teoremos matome, kad Silovo q - pogrupių skaičius yra lygus 1 + kq ir yra pq daliklis. Taigi, Silovo q - pogrupis yra vienintelis - tai pogrupis (b). Tai normalusis pogrupis. Iš Silovo teoremos taip pat matome, kad Silovo p - pogrupių skaičius yra lygus 1 + kp ir yra q daliklis. Šiuo atveju galimi du variantai:
(i) Silovo p - pogrupis (a) yra vienintelis. Tada jis yra normalusis ir G = (ab), t.y. G ≈ Zpq.
(ii) Yra q Silovo p - pogrupių. Tai teisinga tik tada, kada q ≡ 1 (mod p). Kadangi(b) normalusis pogrupis, tai a-1ba Î (b), t.y. a-1ba = br:
α) jeigu r = 1, tai G = (ab) ir G ≈ Zpq.
β) jeigu r ≠ 1, tai rp ≡ 1 (mod q), r **?** 1 (mod q) ir sandaugos formulė axby. azbt = ax+zbyrz+t apibrėžia nekomutatyvią pq eilės grupę G.
Gavome, kad yra galimi tik du pq eilės grupių tipai: tai komutatyvi grupė Zpq ir nekomutatyvi grupė, kai q ≡ 1 (mod p).
Pavyzdys. Tegu p = 2, q = 3. Turime 3 ≡ 1 (mod 2). Gerai mums žinomos 6-os eilės grupės: komutatyvi Z6 ir nekomutatyvi S3, ir sudaro visą grupių, kurių eilė lygi 6, sąrašą.
Dabar aptarkime grupes, turinčias p2q elementų, čia p, q - pirminiai skaičiai. Predėsime apibrėžimu.
Apibrėžimas 4.5 Tegu G - grupė, o A ir B - tokie jos pogrupiai, kad:
(i) A ir B yra normalieji G pogrupiai;
(ii) A ∩ B = < e >;
(iii) A · B = G.
Tada grupę G vadina pogrupių A ir B vidine tiesiogine sandauga: G = A 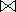 B.
B.
Pavyzdys. Simetrinė grupė S3 yra savo normaliųjų pogrupių B = {id, (12)} ir A = {id, (123), (132)} vidinė tiesioginė sandauga: G = A 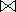 B.
B.
Teorema 4.6 Tegu G - grup4, turinti p2q elementų, čia p ir q - pirminiai. Tada G yra savo Silovo pogrupių vidinė tiesioginė sandauga.
Teorema 4.7 12-osios eilės nekomutatyvioji grupė yra izomorfinė arba A4 , arba D6 , arba Z3 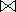 Z4 .
Z4 .
Įrodymas. Tegu G - grup4 ir |G| = 12. Silovo 2 - pogrupis yra izomorfinis arba Z4 , arba Z2 x Z2, o Silovo 3 - pogrupis yra izomorfinis Z3 . Išnegrinėkime visas galimas vidines tiesiogines šių pogrupių sandaugas.
(i) Z4 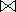 Z3 yra izomorfinė Z4 x Z3 ≈ Z12 .
Z3 yra izomorfinė Z4 x Z3 ≈ Z12 .
(ii) (Z2 x Z2) 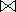 Z3 yra izomorfinė A4 .
Z3 yra izomorfinė A4 .
(iii) Z3 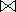 (Z2 x Z2) yra izomorfinė D6 .
(Z2 x Z2) yra izomorfinė D6 .
(iv) Z3 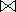 Z4 yra taip vadinama "T" izomorfinė grupė.
Z4 yra taip vadinama "T" izomorfinė grupė.
Įrodyta.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Visų grupių, kurių eilė neviršija 15, veiksmo lenteles galima rasti čia