K[x] laipsnis yra n. Kūno plėtinys F/K vadinamas polinomo f skaidymo kūnu viršK, jeigu egzistuoja tokie elementai r1, ..., rn F, kad f(x) = a(x-r1)...(x-rn) su a K ir F=K(r1,...,r n).
Kaip ir Galua domėjosi palinomų šaknų radimu, taip ir mes paklausime, kokiuose kūnose polinomas įgyja šaknis.Antrame skyriuje mes nagrinėjome kūno plėtinius, gautus prijungiant neredukuojamo polinomo šaknį (visi šie plėtiniai yra paprastieji). Dabar mes apibendrinsim šaknies prijungimo veiksmą ir kalbėsime apie polinomo šaknų prijungimą, t.y. kalbėsime apie algebrinius plėtinius, gaunamus paprastųjų plėtinių pagrindu.
Apibrėžimas 3.1 Tegu K yra kūnas ir polinomo f(x) K[x] laipsnis yra n. Kūno plėtinys F/K vadinamas polinomo f skaidymo kūnu viršK, jeigu egzistuoja tokie elementai r1, ..., rn F, kad f(x) = a(x-r1)...(x-rn) su a K ir F=K(r1,...,r n).
Teorema 3.2 Tegu polinomo f K [x] laipsnis yra n >0. Tada egzistuoja polinomo f skaidymo kūnas F virš K ir [F:K] ≤n!.
Įrodymas. Indukcija pagal n. Jeigu n=1, tai pats kūnas K yra polinomo f skaidymo kūnas virš K. Tegu teorema yra teisinga su visais kūnais L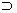 
K ir su bet kokiu polinomu g L[x], kurio laipsnis yra mažesnis už n. Tegu dabar pK[x] yra polinomo f neredukojamas daliklis ir r1 yra polinomo p šaknis. Tada polinomas iš K(r1)[x] turi šaknį kūne K(r1) ir f= (n- r1)g su gK (r1)[x] ir deg g = n-1. Tada pagal indukcijos prielaidą egzistuoja toks polinomo g skaidymo kūnas F/K(r1) virš K(r1), kad [F:K(r1)]≤( n-1)!. Tada nesunku patikrinti, kad F yra polinomo f skaidymo kūnas. Beto, pagal Teoremas 1.8 ir 1.5 turime, kad [F:K]=[F:K(r1)]
[K(r1):K]≤(n-1)!n=n!.
Įrodyta.
Pastebėsime, kad K(r1,..., rn) = K(r1)(r2)...(rn) ir todėl pagal Teorema 1.6 polinomo f skaidymo kūnas yra vienintėlis izomorfizmo atžvilgiu.
Apibrėžimas 3.3 Tegu polinomo f K[x] laipsnis yra n>0, o F- polinomo fskaidymo kūnas. Grupė Gal(F/K) vadinama polinomo f Galua grupė virš K.
Pavyzdys. Žinome, kad kompleksinių skaičių kūnas C yra polinomo x2+1 skaidymo kūnas virš R,todėl polinomo x2+1 Galua grupė virš R yra izomorfinė dviejų elementų grupei Z2. Aišku, kad ir polinomo x2+5 Galua grupė virš Q yra izomorfinė Z2.
Pavyzdys. Nagrinėkime dabar polinomą f = x3 + 5x2 + x + 5 virš baigtinio kūno GF(3). Tada f = x3 1 = (x - 1)(x2 + 1) virš GF(3). Iš polinomo f skaidinio matome, kad polinomo f skaidymo kūnas virš GF(3) sutampa su neredukuojamo virš GF(3) polinomo p = x 2+ 1 skaidymo kūnu. Tegu u yra polinomo p šaknis, easanti kūno GF(3) plėtinyje. Tada GF(3)(u) yra polinomo p skaidymo kūnas, nes p = (x u)(x u`)GF(3)(u) [x], čia u` GF(3)(u). (Tai teisinga, nes polinomas yra įverčio homomorfizmo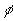 
u : GF(3)(u)[x] → GF(3)(u) branduolyle ir todėl dalijasi iš brandolį ker 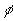u generuojančio polinomo x u ). Taigi, [GF(3)(u) : GF(3)] = 2 ir todėl grupėje Gal(GF(3)(u)/GF(3)) yra tik du elementai ir todėl Gal(GF(3)(u)/GF(3)) ≈ Z2.
Prieš pateikant sudetingesnį pavyzdį, įrodisime lemą.
Lema 3.4 Tegu F/K yra baigtinio matavimo plėtinys ir L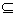 
E yra tarpinai kūnai. Tada [L: E]≤ [E:L] ir, atskiru atviejų, |Gal(F/K)|≤[F:K].
Įrodymas.Indukcija pagal n=[E:L]. Teiginys akivaizdus, kai n=1. Tegu dabar n>1 ir su visais j< n lemos teiginys yra teisingas. Parinkime u E taip, kad u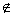
L. Kadangi [E:L]<∞, tai u yra algebrinis virš L (Teorema 1.7) ir u minimaliojo polinomo p L[x] laipsnis yra k>1. Pagal Teoremas 1.5 ir 1.8 turime [L(u):L]=k ir [E:L(u)]=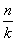
.
Jeigu k<n, tai 1<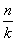 <n ir pagal indukciją [L: L(u)] = [L(u):E] ≤ k 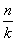= n = [E:L]. Gavome ko siekėme.
Tegu dabar k=n, taigi, E=L(u). Lemos teiginiui įrodyti mums pakanka sukonstruoti injektyvią funkciją tarp grupės L pogrupio E kairiųjų sluoksnių aibės S ir elemento u minimalus polinomo p L[x] skirtingų šaknių aibės T. (Aibėje T yra ne daugiau kaip n elementų, nes deg (p)=n.)
Tegu τE` yra kairysis sluoksnis pogrupio E`≤L` atžvilgiu. Apibrėžkime funkciją ψ :S→T formule ψ(τE`)=τ(u). Ši funkcija apibrėžta korektiškai, nes iš τE`= σE` turime σ=τρ čia ρ E`. Todėl σ(u)= τρ(u)=τ(u), nes iš to, kad u E teisinga ρ(u)=u. Parodysime, kad ψ yra injekcija. Tegu τ(u)= σ(u). Pagal Teoremą 1.5 su kiekvienu ωE turime, kad ω =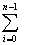 
ai ui, čia a0,...,an-1 L. Tada σ-1τ(ω)=
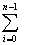aiσ-1 τ(u)i = 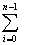aiu-1=ω, taigi σ-1τ =E`. Gavome, kad ψ yra injenktyvi funkcija ir todėl [L`:E`]= |S|≤ |T|≤ n=[E:L].
Jeigu, pagaliau, L=K ir E=F , tai turime |Gal(F/K)|≤[E:L].
Įrodyta.
Dabar išnagrinėsime tokį pavyzdį.
Pavyzdys. Pateiksime polinomo f=x3-5 Q[x] skaidymo kūną ir Galua grupę. Kūne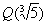 
yra polinomo f šaknis, bet šis kūnas nėra polinomo f skaidymo kūnas, nes jam tik viena polinomo f šaknis. Polinomų žiede 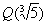[x] turime 
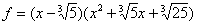ir kvadratinis trinaris 
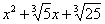yra neredukuojamas virš 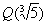. Tegu 
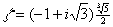. Skaičius ξ yra polinomo f šaknis virš Q, taigi, ξ yra polinomo 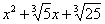šaknis virš 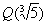. Dabar aišku, kad F=
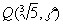yra polinomo x3-5 skaidymo kūnas virš Q. Toliau, pagal eoremas 1.8 ir 1.5, turime [F:Q]= [ 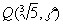: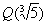][ 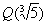:Q]=23 = 3!
Dabar rasime polinomo f Galua grupę. Pagal Teoremą 2.2 šios Galua grupės elementai yra polinomo f šaknių
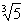, ξ, 
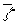, čia 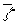- kompleksinio skaičiaus ξ jungtinis, keitiniai. Tegu grupės Gal (F/K) elementas τ kompleksiniam skaičiui priskiria jo jungtinį, o elementas σ cikliškai perstato polinomo šaknis: σ (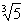)=ξ, σ(ξ)= 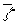, σ( 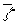)= 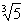ir su visais q Q turime σ(q)=q. Nesunku patikrinti (tai paliekame atlikti skaitytojui), kad σ yra automorfizmas. Automorfizmo σ eilė yra 3, o automorfizmo τ eilė yra 2. Toliau, στ(ξ)= 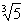, bet στ(ξ)= ξ. Gavome, kad grupė Gal(F/Q) yra nekomutatyvi ir pagaliau pagal Lemą 3.4 turime, kad Gal(F/Q)≤6. Vienintėlė nekomutatyvi grupė, kurios eilė neviršija 6 yra keitinių grupė S3. Taigi, |Gal(F/Q)| ≈S3. Iš tikrųjų, grupėjė yra 6 elementai: idGal(F/K), τ, σ, τ ∙σ, σ ∙τ ir σ ∙σ. Izormorfizmą apibrėžime priskirimu ψ.
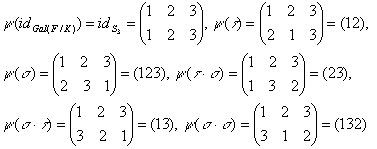
Norint įsitikinti, kad tai izomorfizmas, pakanka palyginti veiksmų lenteles šiose grupėsė:
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ir grupėjė S3:
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|