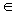K vadina K-homomorfizmu. K izomorfizmas : s : F® F vadinamas kūno F K - automorfizmu: Visų K - automorfizmų aibę pažymėkime Gal(F=K): (Pastebėkime, kad visų kūno F automorfizmų aibė žymi Aut(F); kuri, kaip nesunku parodyti, yra grupė.)
Šiame skyriuje mes apibrėšime Galua grupes. Prancūzų matematikas E. Galua ( Evariste Galois, 1812-1832) domėjosi grupių teorijos taikymu kūnų plėtiniams, apibrėžiamų polinomų pagalba, nagrinėti. Tame tarpe jis norėjo rasti tikslias polinomų išsprendžiamumo radikalais sąlygas. Problema formuluojama taip: ar galima rasti bet kurio laipsnio polinomo šaknų išraiškas, naudojant tik keturis aritmetinius veiksmus ir bet kurio natūralaus laipsnio traukimo šaknies veiksmus iš polinomo koeficientų. Iš pradžių norvegų matematikas N.H. Abelis (N.H. Abel,1802-1829 ) pateikė penktojo laipsnio polinomo su racionaliais koeficientais neišsprendžiamo radikalais pavyzdį, o šiek tiek vėliau E.Galua nurodė tikslią šio rezultato priežastį, kiekvienam polinomui priskirdamas baigtinę grupę. Galua teorija skelbia: polinomas išsprendžiamas radikalais tada ir tik tada, kada jo grupė, kuri ir vadinama Galua grupe, yra išsprendžiama. šiame kurse mes pabandysime tai įrodyti.
Tegu E ir F yra kūno K plėtiniai. Tokį nenulinį kūnų homomorfizmą s :E ® F, kad s (a)=a; su visais a 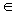K vadina K-homomorfizmu. K izomorfizmas : s : F® F vadinamas kūno F K - automorfizmu: Visų K - automorfizmų aibę pažymėkime Gal(F=K): (Pastebėkime, kad visų kūno F automorfizmų aibė žymi Aut(F); kuri, kaip nesunku parodyti, yra grupė.)
Lema 2.1 Aibė Gal(F=K) yra grupė kompozicijos atžvilgiu. šią grupę mes vadinsime kūno F Galua grupe virš K.
Įrodymas. Mes parodysime, kad Gal(F=K) yra visų kūno F bijekcijų grupės A(F) pogrupis. Turime idFÎGal(F/K); taigi Gal(F=K) nėra tuščia. Tegu dabar q,f 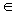Gal(F/k) Tada f q -1yra kūno F automorfizmas, nes dviejų žiedo izomorfizmų kompozicija yra žiedo izomorfizmas. Beto f q-1(a)= f (q -1(a))= f (a)=a su visais a 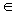K: Taigi, f q-1Î Gal(F/k) yra ir pagal pagrindinę pogrupio savybę [5.7 teiginys,3] turime, kad Gal(F=K) yra grupė.
Įrodyta.
Dabar pateiksime teoremą, kuri taikoma kai kurioms paprastoms Galua grupėms skaičiuoti.
Teorema 2.2 Tegu F=K yra kūno plėtinys ir elemento u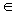 F minimalusis polinomas yra pÎ K[x] : Tada su visais s 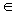Gal(F/k) elementas s (u) taip pat yra polinomo p šaknis. Kitaip sakant, kiekvienas s Î Gal(F/k) yra polinomo šaknų, esančių kūne F; keitinys( perstata).
Įrodyti paliekame skaitytojui.
Pavyzdys. Nagrinėkime kompleksinių skaičių kūną C. Žinome, kad C = R(i) ir polinomo x2+1 šaknys yra i ir -i: Todėl, pagal Teoremą 2.2, grupėje Gal(F=K) yra tik du elementai. Nesunku patikrinti, kad funkcija a+i*b® a-i*b yra kūno C R- automorfizmas, todėl Gal(C/R)» Z2<; nes yra tik viena grupė, turinti du elementus.
Pavyzdys. Nagrinėkime Q(Ö 5) kaip kūno Q plėtinį. Skaičiai Ö 5 ir -Ö 5 yra neredukuojamo polinomo x2-5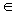 Q[x] šaknys. Pagal Teoremą 2.2 grupėje Gal(Q(Ö 5)/Q) yra tik 2 elementai. Nesunku patikrinti, kad s :Q(Ö 5)® Q(Ö 5),s (a+Ö 5b)= a-Ö 5b yra netrivialusis kūno Q(Ö 5) - automorfizmas, todėl Gal(Q(Ö 5)/Q)»
Z2; nes yra tik viena grupė, turinti du elementus.
Pavyzdys. Nagrinėkime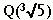 
: Skaičius 
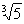yra vienintelis realusis polinomo x3-5 šaknis ir
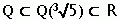: Pagal Teoremą 2.2 grupėje 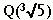yra tik vienas elementas. Matome, kad kiekvienam kūno plėtiniui galima priskirti grupė. Norėtusi žinoti, ką gali mums pasakyti Galua grupė apie patį plėtinį. Mes matėme, kad kiekvienam kūno plėtiniui F=K galima priskirti grupė Gal(F=K) : Nagrinėdami tarpinį kūną KÌ
EÌ F; ką galima pasakyti apie ryšį tarp grupių Gal(F=E) ir Gal(F=K) ?
Teorema 2.3Tegu F=K yra kūno plėtinys. Tada :
1. Su kiekvienu tarpiniu kūnu E grupė E=Gal(F/E) yra grupės Gal(F=K) pogrupis.
2. Su kiekvienu grupės Gal(F=K) pogrupiu H aibė H={v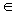 F|s (v)=v su visais s 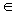H } yra tarpinis plėtinio F=K kūnas.
Įrodymas. (1) Tegu E yra tarpinis kūnas. Tada Gal(F/E)={ s 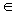Aut(F)|s (b)=b su visais b 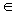E } 
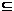{ s 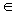Aut(F)|s (a)=a su visais a 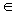K}. Taigi, Gal(F=E) yra A(F) pogrupis, esantis grupėje Gal(F=K) ir E=Gal(F=E) yra Gal(F=K) pogrupis, E =Gal(F=E) <Gal(F=K) ;
(2) Tegu H <Gal(F=K) . Kadangi KÍ H; tai H yra netuščia, turinti 0 ir 1.Tada su visais u,v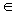 Hturime s (u-v)=s (u)-s (v)=u-v ir s (uv)=s (u)s (v)=uv su visais s 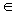H Taigi, u-v ir uv priklauso H ir todėl H yra F požiedis. Beto, su visais 0¹ uÎ H turime s (u-1)= s (u) 1=u-1 taigi u-1Î H: Gavome, kad H yra kūno F pokūnis, turintis K:
Įrodyta.
Jeigu H yra grupės Gal(F=K) pogrupis, tai H vadinsime grupe H apibrėžtu kūnu kūne F: Taigi mes jau žinome, kaip kiekvienam tarpiniam kūnui E priskirti grupės Gal(F=K) pogrupį E ir kaip kiekvienam grupės Gal(F=K) pogrupiui H priskirti tarpinį kūną H; esantį tarp F ir K: Norėtųsi žinoti, ar šie priskirimai apibrėžia abipus vienareikšmę atitiktį tarp plėtinio F=K tarpinių kūnų ir grupės Gal(F=K) pogrupių. Plėtinio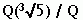 
Pavyzdys rodo, kad ne visada. Tada norėtųsi žinoti tas sąlygas kada taip yra.
Dabar pateiksime kūno plėtinio F=K ir šios atitikties pagrindinius teiginius, kurių įrodymą palieku skaitytojams.
Teiginiai:
1. F=(idF);
2. K'=Gal(F/K) ;
3. (idF)=F ;
4. Jeigu L ir E yra tokie tarpiniai kūnai, kad L 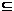M; tai M<L;
5. Jeigu H ir J yra tokie grupės Gal(F/K) pogrupiai, kad H < J; tai J yra H pokūnis ;
6. Su kiekvienu tarpiniu kūnu L ir kiekvienu pogrupiu H<Gal(F/K) turime L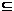 (L)=L ir H<(H)=H;
7. Su kiekvienu tarpiniu kūnu L ir kiekvienu pogrupiu H<Gal(F/K) turime L=(L)=L ir H=(H)=H .
Šiuos teiginius galime apibendrinti tokia diagrama:
|
F |
® |
<idF> |
Gal(F/K) |
® |
K | |
|
U |
L |
V |
D | |||
|
M |
® |
M |
J |
® |
J | |
|
U |
|
L |
V |
D | ||
|
L |
® |
L |
H |
® |
H | |
|
U |
|
L |
V |
D | ||
|
K |
® |
Gal(F/K) |
<idF> |
® |
F |
Pastebėsime, kad iš Teiginio 6 turime, kad su visais tarpiniais kūnais L teisinga L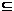 Lir su kiekvienu pogrupiu H <Gal(F=K) teisinga H < H: Tarpinį kūną vadinsime uždaru, jeigu L = L: Panašiai, pogrupį H <Gal(F=K) vadinsime uždaru, jeigu H = H:
Teorema 2.4 Tegu F=K yra kūno plėtinys. Egzistuoja abipus vienareikšmė atitiktis tarp uždarų tarpinių kūnų ir uždarų grupės Gal(F=K) pogrupių E® E<Gal(F/K) su kiekvienu uždaru tarpiniu kūnu E:
Įrodymas. Parodysime, kad ši atiktis yra injekcija. Tegu E ir L yra tokie du tarpiniai kūnai, kad E = L: Bet E ir L yra uždari, todėl E = E = L = L: Dabar parodysime, kad atitiktis yra surjekcija. Su kievienu uždaru pogrupiu H <Gal(F=K) turime H = H = (H) ir todėl kūną H atitinka pogrupis H.
Įrodyta.
Svarbu pastebėti, kad Gal(F=K) nebūtinai sutampa su K ir gali būti didesnis už K: Kitaip sakant, kūnas K gali būti ir ne uždaras.
Apibrėžimas 2.5 Tegu F=K yra kūno plėtinys. Kūnas F vadinamas Galua kūnu virš K; jeigu Gal(F=K) = K: Šiuo atveju kūno plėtinys F=K yra vadinamas Galua plėtiniu.