Paskaitų ciklas remiasi tiek bendruoju algebros kursu, skaitomu informatikams pirmame ir antrame semestruose, tiek ir diskretinės matematikos kursu, kuris skirtas baigtinėms algebrinėms struktūroms, skaitomu trečiame semestre.
Apibrėžimas 1.1 Jei K Í F ir K, F yra kūnai tų pačių operacijų atžvilgiu, tai kūnas K vadinamas kūno F pokūniu, o kūnas F vadinamas kūno K plėtiniu ir žymima F/K.
Prisiminkime vektorinės erdvės apibrėžimą.
Apibrėžimas 1.2 Vektorinė erdvė virš kūno K yra tokia adaptyvioji Abelio grupė V, kad egzistuoja funkcija * : K x V ® V, pasižymi savybėmis:
1.(a * b) * x = a * (b * x) su visais a, b Î K ir x Î V.
2.(a + b) * x = a * x + b * x su visais a,b Î K ir x Î V.
3.a * (x + y) = a * x + b * y su visais a,b Î K ir x Î V.
4.1 * x = x su visais x Î V.
Sekanti lema mums parodys, kad žinios iš tiesinės algebros kurso palengvina mūsų kūnų plėtinių tyrimą.
Lema 1.3 Jeigu F/K yra kūno plėtinys, tai F yra vektorinė erdvė virš K.
Įrodymas. Kaip žinia, kūnas F yra adityvioji Abelio grupė. Funkciją * : K x F ® F galima apibrėžti tokiu būdu: k * x = kx, čia antroji sandauga tai kūno F elementų sandauga. Dabar nesunku tiesiogiai patikrinti, kad taip apibrėžta funkcija * tenkina apibrėžimo 1.2 savybes 1-4 ir tuo pačiu F tampa vektorine erdve virš kūno K.
Įrodyta.
Taigi, jei F/K yra kūno plėtinys, tai mes galime apibrėžti šio plėtinio laipsnį kaip vektorinės erdvės dimensiją: [F : K] = dimK(F). Tokiu būdu, [F : K] yra vektorinės erdvės F virš kūno K bazėje esančių elementų skaičius.
Prisiminkime. Tegu V yra vektorinė erdvė virš kūno K. Tegu B yra netuščias V poaibis. Tada K tiesiniu apvalkalu, generuotu aibe B (arba tiesiog tiesiniu apvalkalu) vadiname aibę, kurios elementais yra visos baigtinės tiesinės kombinacijos
a1v1 + ×× × + anvn su visais a1, ,an Î K ir v1, ,vn Î B.
Aibė B vadinama tiesiškai nepriklausoma virš K, jeigu su visais n Î N ir su visais v1, ,vn Î B vieninteliu lygties
a1v1 + ×× × + anvn = 0
sprendiniu a1, ,an Î K atžvilgiu yra a1 =a2 = ×× × = an =0.
Aibė B Í V vadinama vektorinės erdvės V K baze (arba tiesiog baze), jeigu ji yra tiesiškai nepriklausoma virš K, ir tiesinis apvalkalas, generuotas aibe B, sutampa su V.
Tegu dabar F/K yra kūno plėtinys yra u Î F. Žymeniu K(u) žymėsime mažiausią kūno F pokūnį, kuriame yra ir kūnas K ir elementas u. Taigi su kiekvienu kūno F tokiu pokūniu E, kad K Í E ir u Î E turime K(u) Í E. Plėtinį K(u)/K vadina paprastuoju plėtiniu. Panašiai ir baigtinių elementų u1, ,un Î F rinkiniui mes galime apibrėžti kūną K (u1, ,un), kuris yra mažiausias kūno F pokūnis, kuriame yra ir kūnas K ir elementai u1, ,un. Bendru atveju, su kiekviena aibe X Í F, mes galime apibrėžti kūną K(X) kaip mažiausią kūno F pokūnį, kuriame yra ir kūnas K ir aibė X.
Visų pirma, mes atidžiau pažiūrėsime į paprastuosius plėtinius. Tegu dabar F/K yra kūno plėtinys ir u Î F. Tegu egzistuoja įverčio homomorfizmas fu : K [x] ® F, apibrėžtas formule fu
= 
su visais n Î N ir su visais a0,
,an Î K. (Tikrai nesunku įsitikinti, kad fu yra homomorfizmas, pastebėjus, kad fu (p) = p (u) su visais p Î K [x].) Be to, nesunku matyti, kad Imfu Í K (u) , nes K (u) yra uždaras tiek sudėties, tiek sandaugos atžvilgiu.
Apibrėžimas 1.4 Tegu F/K yra kūno plėtinys. Elementas u Î F vadinamas algebriniu virš kūno K , jeigu egzistuoja toks nenulinis p Î K [x], kad p (u) = 0. (Tai ekvivalentu sąlygai ker(fu) ¹ 0.) Elementas u Î F vadinamas transcendentiniu virš kūno K, jeigu jis nėra algebrinis virš K. (Tai ekvivalentu sąlygai ker(fu) = 0. ) Kūnas F vadinamas transcendentiniu virš K, jeigu F nėra algebrinis virš K.
Teorema 1.5 Tegu F/K yra kūno plėtinys ir u Î F.
1. Jeigu u yra transcendentinis virš K, tai K (u) 
K (x).
2. Jeigu u yra algebrinis virš K, tai K (u) K [x] / á pñ su visiškai apibrėžtu neredukuojamu polinomu p Î K [x].
Be to, aibė {1, u2,
, un-1}, čia n = [K(u) : K] = deg(p), yra K (u) bazė.
Įrodymas.(1) Tegu u yra transcendentinis virš K. Tada su kiekvienu nenuliniu polinomu g Î K [x] turime g (u) = fu (g) ¹ 0 ir todėl g (u) turi turėti atvirkštinį elementą kūne K (u) : t.y. su visais f, g Î K [x], kai g ¹ 0 turime f(u) / g(u) Î K (u). Dabar mes galime apibrėžti homomorfizmą 
: K (x)® K (u), (f/g) = f (u) / g (u) su visais f/g Î K (x). yra netrivialus homomofizmas, todėl jis yra monomorfizmas. Kadangi Im yra kūno K (u) pokūnis, kuriame yra ir u, ir K, tai Im turi sutapti su K (u). Taigi yra izomorfizmas.
(2)Tegu u yra algebrinis virš K. Tada ker(fu) = ápñ su nenuliniu p Î K [x]. Mes parodysime, kad p turi būti neredukuojamas ir tuo pačiu ápñ yra maksimalusis idealas polinomų žiede K [x]. Jeigu priešingai, fg = p su f, g Î K [x] ir deg f ir deg g yra griežtai mažesni už deg p, tai f (u)g (u) = p (u) = 0. Bet F yra kūnas ir todėl arba f (u) = 0 arba g(u) = 0, t.y. arba f Î ker(fu) arba g Î ker(fu). Taigi arba f = pq arba g = pq su qÎ K [x]. Bet tai prieštarauja nelygybėms tarp polinomų p, f ir g laipsnių ir tai rodo, kad polinomas turi būti neredukuojamas.
Kadangi p yra neredukuojamas, tai Im(fu K [x] / ápñ yra kūnas, kuriame yra ir kūnas K ir elementas u. Mes turime Im(fu) Í K (u) Í Im(fu), todėl K (u) K [x] / ápñ.
Dabar parodysime, kad aibė U = {1, u2, , un-1} yra K (u) bazė virš K, čia n = deg(p). Su kiekvienu w Î K (u) egzistuoja toks f Î K [x], kad fu (f) = w. Iš Dalybos su liekana teoremos turime, kad f = pg + r, su q, r Î K [x] ir r = a0 + a1x + ×× × + an-1xn-1, čia a0, a1, an-1 Î K. Kadangi pq Î ker(fu), tai turime, kad w = fu (f) = a0+ a1u + ×× × + an-1un-1. O tai rodo, kad U yra generuojanti K (u) sistema. Maža to, jeigu a0 + a1u + ×× × + an-1un-1 = 0, čia a0, a1, an-1 Î K, tai a0 + a1x + ×× × + an-1xn-1 Î ker(fu). Kadangi paskutinio polinomo laipsnis mažesnis už polinomo p laipsnį, tai būtinai a0 + a1x + ×× × + an-1xn-1 = 0 (mažiausio laipsnio nenulinis polinomas, esantis ideale ker(fu) yra p). Gavome, kad a0 = a1 =×× × = an-1 = 0 ir todėl U yra tiesiškai nepriklausoma ir tuo pačiu K(u) bazė.
Įrodyta.
Jeigu F/K yra kūno plėtinys ir u Î F yra algebrinis virš K, tai minimaliuoju elemento u polinomu vadiname tokį vienintelį normuotą neredukuojamą polinomą p Î K [x], kad p (u) = 0. Aišku, kad elemento u minimalusis polinomas yra vienintelis normuotas idealo ker(fu) generatorius. Elemento u laipsniu virš K vadinsime jo minimalaus polinomo p laipsnį.
Svarbi paskutinės teoremos išvada yra ta, kad, jeigu u Î F/K yra n-tojo laipsnio algebrinis elementas virš kūno K, tai kiekvieną elementą c Î K (u) vieninteliu būdu galima reikšti elementų 1, u, u2, , un-1 tiesine kombinacija
c = a0 + a1u + ×× × + an-1un-1,
čia a0, a1, an-1 Î K.
Pavyzdys. Nagrinėkime F = Q 
. Kadangi x3 2 yra neredukuojamas virš Q, tai pagal Teoremą 1.5 aibė 
yra F bazė virš Q. Tada kiekvienas elementas v Î F vieninteliu būdu gali būti užrašytas aibės elementų tiesine
kombinacija : v = a0 + a1
+ a2
, čia a0 , a1 , a2 Î Q.
Dabar mes palyginsime įvairius kūno K plėtinius. Visų pirma, mes pasinaudosime įverčio homomorfizmu paprastiems algebriniams plėtiniams klasifikuoti izomorfizmo atžvilgiu.
Teorema 1.6 Tegu E/K ir F/K yra du kūno plėtiniai, o u Î E ir v Î F yra algebriniai elementai virš K. Šie elementai u ir v yra šaknimis vieno ir to pačio neredukuojamo polinomo p Î K [x] tada ir tik tada, kada egzistuoja toks kūnų izomorfizmas y : K (u) ® K (v), kad y(u) = v ir y(a) = a su visais a Î K.
Įrodymas. Tegu u ir v yra neredukuojamo p Î K [x] šaknys. Tada pagal Teoremą 1.5 fu ir fv indukuoja izomorfizmus : K [x] / ápñ ® K (u) ir 
: K [x] / ápñ ® K (v), kurie tenkina lygybes (x) = u, (a) = a ir (x) = v, (a) = a su visais a Î K. Taigi y = 
yra ieškomasis homomorfizmas.
Priešingai, tegu egzistuoja izomorfizmas y : K (u) ® K (v). Tada yfu = fv ir ker(fu) = ker(fv) Í K [x]. Bet K [x] pagrindinių idealų sritis, todėl ker(fu) = ápñ, čia p neredukuojamas virš K polinomas, bei u ir v yra šio polinomo šaknys.
Įrodyta.
Pagrindinė Teoremos 1.6 išvada yra ta, kad paprastasis algebrinis plėtinys K (u) yra apibrėžtas vienareikšmiškai izomorfizmo tikslumu. Apie šį plėtinį dar sako, kad jis gaunamas prijungiant prie kūno K neredukuojamą polinomo pÎ K [x] šaknį. Nereikia galvoti, kad, prijungus vieną neredukuojamo polinomo šaknį, prijungsim ir likusias, t.y. paprastieji plėtiniai K (u) ir K (v) iš Teoremos 1.6 ne visada sutampa. Pavyzdžiu galėtų būti neredukuojamas virš Q polinomas x4 2. Aišku, kad plėtinyje Q 
Q , čia 
- aritmetinė ketvirto laipsnio šaknis iš 2, nėra kompleksinių polinomo x4 2 šaknų ± i, t.y. Q ¹ Q 
, nors šie kūnai ir yra izomorfiški.
Dabar mes įrodysime teoremą, kuri nesunkiai leidžia mums nustatyti plėtinio algebriškumą.
Teorema 1.7 Jeigu F yra baigtinio laipsnio kūno K plėtinys, tai F yra algebrinis kūno K plėtinys, generuojamas baigtine aibe virš K.
Įrodymas. Tegu [F : K] = n. Tada su kiekvienu uÎ F aibė {1, u, u2, , un}, turinti n + 1 elementą, yra tiesiškai priklausoma, t.y. egzistuoja tokie ne visi lygūs nuliui a0, a1, an-1 Î K, kad:
a0 + a1u + ×× × + anun = 0,
o tai rodo, kad u yra algebrinis virš K. Tai teisinga su kiekvienu uÎ F ir todėl F yra algebrinis virš K. Toliau, jeigu {v1, , vn} yra F bazė virš K, tai F = K (v1, , vn), o tai rodo, kas F yra generuojamas baigtine aibe virš K.
Įrodyta.
Atvirkštinis Teoremai 1.7 teiginys nėra teisingas. Pavyzdžiu galėtų būti visų algebrinių virš Q kompleksinių skaičių aibė 
. Ši aibė yra kūnas, nes jeigu a, bÎ, tai a + b, ab, a-1, b-1 priklauso Q(a, b). Pagal Teoremą 1.7 kūnas Q(a, b) yra algebrinis kūno Q plėtinys, todėl visi nagrinėjami elementai priklauso . Kūną vadina algebrinių skaičių kūnu. Turime, kad su kiekvienu natūraliuoju pirminiu skaičiumi p ir primityviąja p-tojo laipsnio šaknimi iš vieneto V teisinga tai, kad Q(V) Ì ir [Q(V):Q] = p 1. Taigi plėtinio laipsnis [:Q ] = ¥ .
Toliau, jeigu F/K yra kūno plėtinys ir E yra kūno F pokūnis, kuriame yra kūnas K, K Í E Í F, tai kūnas E vadinamas tarpiniu kūnu.
Teorema 1.8 Tegu F/K yra kūno plėtinys, o E yra tarpinis kūnas. Tada [F : K] = [F : E] = [E : K] ir [F : K] yra baigtinis tada ir tik tada, kada ir [F : E], ir [E : K] yra baigtiniai.
Įrodymas. Tegu B yra E bazė virš K, o B yra F bazė virš E. Dabar pakanka parodyti, kad BB = {xy|xÎ B, y Î B} yra F bazė virš K ir |BB| = |B| × |B|.
Parodysime, kad BB generuoja F. Tegu z Î F. Tada egzistuoja tokie y1, ..., yn Î B ir a1,
, an Î E, kad z = 
. Bet su kiekvienu ai Î E egzistuoja tokie xi,1, ...,
Î B ir ci,1, ...,
Î K kad ai = 
. Iš čia turime
z =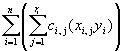 
ir todėl BB generuoja F.
Parodysime, kad BB yra tiesiškai nepriklausoma virš K. Tegu x1,
, xm Î B , y1, ..., yn Î B ir c1,1,c1,2 , ...,cm, nÎ K yra tokie, kad 
= 0. Aibė B yra tiesiškai nepriklausoma ir todėl F bazė virš K.
Įrodyta.
Iš Teoremos 1.5 turime: jeigu u Î F yra algebrinis elementas virš K, o E yra tarpinis kūnas, tai
[E(u) : E] £ [K(u) : K].
Iš tikrųjų, jeigu [K(u) : K] = n, tai elemento u minimalusis polinomas p Î K [x] yra taip pat ir polinomas iš E [x]. Taigi, elementas u yra n-tojo laipsnio polinomo virš kūno E šaknis, todėl u minimalaus polinomo virš E laipsnis yra ne didesnis už n. Ši pastaba padės mums įrodyti
Teorema 1.9 Tegu F/K yra kūno plėtinys, o E yra visų kūno F algebrinių elementų virš K aibė. Tada E yra kūno pokūnis, algebrinis virš K.
Įrodymas. Tegu u, v Î E yra nenuliniai. Tada
[K(u, v) : K] = [K(u, v) : K(u)][K(u) : K] £ [K(v) : K][K(u) : K] < ¥. Pagal Teoremą 1.7 turime, kad K(u, v) yra algebrinis virš K. Taigi K(u, v) Í E ir. Kadangi u v, uv Î K(u, v) Í E, turime, kad E yra požiedis kūne F. Turime taip pat ir tai, kad su kiekvienu nenuliniu u Î E elementas u-1 Î K(u) Í E ir todėl E yra kūno F pokūnis ir pagal apibrėžimą algebrinis virš K.
Įrodyta.
Teorema 1.10 Tegu F/K yra kūno plėtinys, o E yra toks tarpinis kūnas, kad F yra algebrinis virš E, o E yra algebrinis virš K. Tada F yra algebrinis virš K.
Įrodymas. Tegu u Î F. Elementas u yra algebrinis virš E, todėl egzistuoja toks n Î N ir tokie b0, , bn Î E, kad b0 + b1u + ×× × + bnun = 0. Kūnas E yra algebrinis virš K, todėl bj su visais j yra algebrinis virš K ir tuo pačiu metu virš bet kurio tarpinio tarp E ir K kūno. Taigi, kūnų sekoje
K Í K(b0) Í K(b0, b1) Í Í K(b0, , bn) Í K(b0, , bn, u)
esantys kūnai pagal Teoremą 1.5 yra iš kairės esančių paprastieji algebriniai plėtiniai, nes kiekvieno iš šių plėtinių laipsnis yra baigtinis. Tada pagal Teoremą 1.8 turime
[K(b0, , bn, u) : K] = [K(b0, , bn, u) : K(b0, , bn)] ×× ×[K(b0) : K] < ¥.
Pagal Teoremą 1.7 K(b0, , bn, u) yra algebrinis virš K, tuo pačiu metu ir u turi būti algebriniu virš K.
Įrodyta.
Iš Teoremos 1.10 turime svarbią visų algebrinių virš Q skaičių kūno savybę, kuri sugretina jį su kompleksinių skaičių kūnu. Tikrai, bet kuris nenulinio laipsnio polinomas f(x) Î turi šaknį kūne. Norėdami tai parodyti, nagrinėkime kūnų grandinę: Q ÌÍ(a), čia a - kompleksinė polinomo f(x) šaknis. Paprastasis plėtinys a)/ yra algebrinis ir pagal Teoremą 1.10 plėtinys (a)/ Q irgi yra algebrinis, tuo pačiu ir elementas a yra algebrinis virš Q, t.y. (a) = ir aÎ.
Algebrinis kūno K plėtinys `K vadinamas algebriškai uždaru kūnu virš K, jeigu bet kuris nenulinio laipsnio polinomas f(x) Î K [x] turi šaknį kūne `K.
yra algebriškai uždaras virš Q, bet C nėra algebriškai uždaras kūnas virš Q (jis nėra algebriškai uždaras net virš ): C yra algebriškai uždaras virš R.
Svarbi savybė: virš bet kurio kūno K egzistuoja algebriškai uždaras kūnas ir jis yra vienintelis plėtinių izomorfizmo tikslumu, t.y. jeigu K ir K yra algebriškai uždari virš K, tai egzistuoja toks kūnų izomorfizmas y : K ® K, kad y (a) = a su visais a Î K.