KŪNŲ TEORIJA

• 1. Kūnų plėtiniai
• 2. Galua grupės
• 3. Polinomų Galua grupės
• 4. Mažos eilės grupių klasifikacija
• 5. Fundamentalioji teorema
• 6. Separabilusis ir normalusis plėtinys
• 7. Klasikiniai brėžimo skriestuvu ir liniuote uždaviniai

Sekdami pitagoriečiais ( V a. pr.Kr.), senieji graikai "skaičiais" vadino tik sveikuosius skaičius ir racionaliuosius skaičius. Tačiau domėdamiesi aristokratijos simboliu - geometrinio vidurkio dydžiu a : b = b : c susidūrė su iracionalumu: kam yra lygus dviejų šventųjų skaičių 1 ir 2 geometrinis vidurkis ?( Pats skaičius buvo pitagoriečių filosofinio misticizmo pagrindas: prisiminkime kad ir jų posakį " viskas yra skaičius"). Geometrinį vidurkį formuluodami geometriškai: "kam yra lygi kvadrato įstrižainė?" - teko pripažinti, kad šis santykis nėra "skaičius". Tai griovė buvusią aritmetikos ir geometrijos harmoniją. Tik Eudokso ( 408 - 355 m.pr.Kr.) santykių teorija "įveikė" šią graikų matematikos "krizė": algebriniai dydžiai buvo reiškiami geometriškai, pavyzdžiui p2 buvo reiškiama kvadrato, kurio plotas yra lygus 2; kraštine, o visos algebrinės operacijos buvo apibrėžiamos geometriškai. Tai buvo savotiškas iracionaliųjų skaičių pripažinimas. Ir tai teikė vilties, kad šių "brėžiamų" skaičių jiems pakaks savo reikmėms. Net žymiesiems savo brėžimo skriestuvu ir liniuote uždaviniams: kubo dvigubinimo, kampo trisekcijos, skritulio kvadratūros,- išspręsti. Dabar mes pamatysime, kodėl šios jų viltys nepasiteisino. Tegu turime liniuotė, kurios ilgis bus 1; ir skriestuvą, kuriuo galime brėžti bet kurio spindulio apskritimus. Skaičių ( tiksliau būtų atkarpą, kurios ilgis yra šis skaičius) vadinsime brėžiamu, jeigu jis yra 1 arba jį galima nubrėžti atlikus tik šiuos veiksmus:

- sujungti du brėžiamus taškus atkarpa;

- brėžti apskritimą, kurio centras yra brėžiamame taške ir spindulys yra brėžiamas skaičius.

Apibrėžimas 7.1 Tegu K yra realiųjų skaičių R pokūnis. Dekarto sandaugą K x K Ģ R x R vadinsime K - plokštuma. Tiese K - plokštumoje vadinsime tiesę, einančią per du K - plokštumos taškus. Ši tiesė yra reiškiama lygtimi

Apskritimu K- plokštumoje vadinsime apskritimą, kurio centras yra K- taške, o spindulys yra iš K: šis apskritimas yra reiškiamas lygtimi

Lema 7.2 Tegu L₁ ¹ L₂ yra dvi K - tiesės ir C₁ ¹ C₂ du K- apskritimai. Tada

(1) L₁ Ē L₂ = Ę arba turi vieną bendrą K- tašką;

(2) L₁ Ē C₁ = Ę arba turi vieną, arba turi du K (Ös)- taškus, čia s Ī K;

(3) C₁ Ē C₂ = Ę arba turi vieną, arba turi du K (Ös)- taškus, čia s Ī K:

Įrodymas. Sankirtų taškai gaunami sprendžiant arba tiesinių lygčių sistemą su koeficientais iš K; arba vienos tiesinės ir vienos kvadratinės lygties, arba dviejų kvadratinių lygčių sistemas su koeficientais iš K: šios sistemos suvedamos blogiausiu atveju į vieno nežinomojo kvadratinės lygties su koeficientais iš K sprendimą. Detales paliekame skaitytojui.

Įrodyta.

Lema 7.3 (1) Jeigu a ir b yra brėžiami skaičiai, tai ir a ± b; a × b ir a ¤ b ,( b ¹ 0 ) yra brėžiami.

(2) Jeigu a > 0 yra brėžiamas, tai ir Öa yra brėžiamas.

Įrodymas. (1) Iš mokyklos laikų mokame brėžti tiesė, einančią per duotą tašką ir lygiagrečią arba statmeną duotai tiesei. žinome taip pat kaip brėžti a ± b: Norint brėžti a × b; viename smailaus kampo su viršūne O spindulyje reikia atidėti taškus A ir B taip, kad OA = 1 ir OB = a (tegu a > 1), o kitame spindulyje - tašką C taip, kad OC = b. Nubrėžę tiesę, einančią per tašką B ir lygiagrečią atkarpai AC gausime susikirtimo tašką D taško C spindulyje. Iš trikampių OAC ir OBD panašumo gauname OA ¤ OC = OB ¤ OD ) Ž 1 ¤ b = a ¤ OD Ž OD = a × b .

Norint nubrėžti skaičių 1¤a; a > 1; reikia smailiojo kampo viename spindulyje atidėti vienetinė atkarpą OA ir atkarpą OB = a; o kitame spindulyje atkarpą OC = 1: Nubrėžė tiesė, einančią per tašką B ir lygiagrečią atkarpai AC gausime susikirtimo tašką D taško C spindulyje. Tada gauname OA ¤ OC = OB ¤ OD ) Ž 1 ¤ 1 = a ¤ OD Ž OD = 1 ¤ a : Dabar mokėsime brėžti ir skaičių a × 1 ¤ b = a ¤ b :

(2) Brėžiame a +1 skersmens apskritimą. Jo skersmenyje AB taip atidedame tašką C; kad AC = a ir CB = 1: Iš taško C iškeliame statmenį, kuris kerta apskritimą taške D: Tada AC ¤ CD = CD ¤ CB Ž CD² = AC × CB Ž CD = Öa:

Įrodyta.

Teorema 7.4 (Pagrindinė brėžimo teorema). (1) Brėžiamų skaičių aibė yra kūnas.

(2) Skaičius a yra brėžiamas tada ir tik tada, kada jis yra plėtinyje

Įrodymas. (1) Tai tiesioginė Lemos 7.3 (1) išvada.

(2) Iš (1) matome, kad brėžiamų skaičių kūnas yra Q plėtinys (pagaliau Q yra mažiausias kūnas turintis sveikąjį 1). Iš Lemos 7.3 (2) turime, kad visi skaičiai iš Q(Öa₁,..., Öa_r) yra brėžiami. Iš kitos pusės pagal Lemą 7.2 kiekvienas brėžiamas skaičius yra kūne Q(Öa₁,..., Öa_r).

Įrodyta.

Išvada 7.5 (Pagrindinė brėžimo sąlyga) Jeigu a yra brėžiamas skaičius, tai a yra algebrinis virš Q ir plėtinio Q(a) ¤ Q laipsnis [Q(a) : Q] yra lygus 2^m.

Įrodymas. Jeigu a yra brėžiamas skaičius, tai iš Teoremos 1.8 kūnų grandinei Q Ģ Q(a) Ģ Q(Öa₁,..., Öa_r) mes žinome, kad [Q(a) : Q] yra [Q(Öa₁,..., Öa_r): Q] = 2^r daliklis.

Įrodyta.

Dabar galime kalbėti apie klasikinių brėžimo skriestuvu ir liniuote uždavinių išsprendžiamumą.

Teiginys 7.6 Negalima skriestuvu ir liniuote nubrėžti kubą, kurio tūris dvigubai didesnis už duotojo kubo tūrį.

Įrodymas. Iš tikrųjų mums pakanka parodyti, kad negalima nubrėžti kubo, kurio tūris yra lygus 2. Tam reikia mokėti nubrėžti kubinės lygties x³ - 2 = 0 šaknį. Pagal Eizenšteino ( F. G. M. Eisenstein, 1823-1852) kriterijų (kai p = 2) polinomas f (x) = x³ - 2 yra neredukuojamas virš Q. Todėl, kaip žinome, [Q(³Ö2):Q] = 3 ir pagal Pagrindinė brėžimo sąlygą turime, kad skaičius ³Ö2 nėra brėžiamas.

Įrodyta.

Teiginys 7.7 Negalima skriestuvu ir liniuote bet kurį kampą padalyti į tris lygias dalis.

Įrodymas. Aišku, kad kampo brėžimas yra ekvivalentus šio kampo trigonometrinių funkcijų reikšmių brėžimui. Taigi, norėdami padalyti kampą - į tris dalis, turėtume mokėti nubrėžti lygties cos a = 4 cos³ a ¤ 3 -3 cos a ¤ 3 sprendinį. Pavyzdžiui, jeigu a = 60°, tai mes turėtume mokėti nubrėžti lygties 8x³-6x-1 = 0 sprendinį. Bet polinomas g (x) = 8x³-6x-1 neturi racionaliųjų šaknų (o jomis galėtų būti tik skaičiai ±1; ±1 ¤ 2; ±1 ¤ 4; ±1 ¤ 8; bet patikrinus taip nėra), todėl jis yra neredukuojamas virš Q. Taigi, [Q(cos 20°) : Q] = 3 ir pagal Pagrindinę brėžimo sąlygą turime, kad skaičius cos 20°; o tuo tarpu ir a ¤ 3 = 20° nėra brėžiamas.

Įrodyta.

Teiginys 7.8 Negalima skriestuvu ir liniuote nubrėžti kvadratą, kurio plotas būtų lygus skritulio plotui.

Įrodymas. Norėdami nubrėžti kvadratą, kurio plotas yra lygus skritulio, kurio spindulys yra r; plotui, turėtume mokėti nubrėžti lygties x² - p = 0 sprendinį. Bet skaičius p yra transcendentinis (pirmasis tai įrodė F.Lindemanas (1852-1939) 1882 metais), todėl polinomas h (x) = x²- p yra neredukuojamas virš Q ir pagal Pagrindinę brėžimo sąlygą turime, kad skaičius Öp nėra brėžiamas.

Įrodyta.

Aptarkime dar vieną klasikinį brėžimo skriestuvu ir liniuote uždavinį: ar galima įbrėžti į apskritimą taisyklingąjį n-kampį? Aišku, jeigu apskritimo spindulį laikysime lygiu 1; o centru pasirinksime koordinačių pradžią, tai reikia mokėti brėžti lygties xⁿ - 1 sprendinius. Pažiūrėkime, kada tai galima padaryti. Visų pirma pastebėsime, kad polinomas xⁿ - 1 yra redukuojamas:

Lema 7.9 Jeigu p yra pirminis skaičius, tai polinomas x^p-1+x^p-2+ × × × +x+1 yra neredukuojamas virš Q ir plėtinio Q(e^2pi/p) / Q laipsnis [Q(e^2pi/p) : Q] = p-1:

Įrodymas. Kai n = p; lygybėje (*) atlikime kintamųjų keitinį t = x - 1 :

Tada

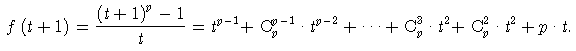
Žinome, kad Cⁱ_p dalijasi iš p su visais 1 £ i £ p - 1. Tada pagal Eizenšteino kriterijų polinomas f (t + 1) ; o tuo pačiu ir polinomas x^p-1+x^p-2+ × × × +x+1; yra neredukuojamas virš Q: Iš Išvados 6.4 turime, kad neredukuojami polinomai virš Q yra separabilūs, todėl [Q(e^2pi/p) : Q] = deg ( x ^p-1 + x ^p-2 + × × × + x + 1) = p - 1

Priminsime, kad e^2pi/p yra polinomo x^p - 1 = 0 šaknis.

Įrodyta.

Lema 7.10 Tegu p - nelyginis pirminis skaičius. Tada  [Q (cos2p/p) É Q] = (p-1)/2

Įrodymas. Tegu p - nelyginis pirminis skaičius. žinodami lygybę

e^2pi/p = cos2p/p + i×sin2p/p , matome, kad norint įbrėžti į apskritimą taisyklingąjį p - Kampį, reikia mokėti brėžti cos2p/p. Turime Q(e^2pi/p) É Q(cos2p/p) É Q. Skaičius e^2pi/p yra lygties x² - 2cos2p/p × x + 1 = 0 sprendinys, be to šis skaičius yra kompleksinis (nepriklauso R). Todėl plėtinio Q(e^2pi/p) / Q(cos2p/p) laipsnis [Q(e^2pi/p) : Q(cos2p/p)] = 2. Pagal Teoremą 1.8 kūnų grandinei Q(e^2pi/p) É Q(cos2p/p) É Q turime  [Q (cos2p/p) É Q] = (p-1)/2

Įrodyta.

Teiginys 7.11 Tegu p yra pirminis skaičius. Jeigu į apskritimą galima įbrėžti taisyklingąjį p - kampį, tai , t.y. pirminis p yra pirminis Ferma ( P.Fermat,1601-1665) skaičius.

Įrodymas. Jeigu mes galime įbrėžti į apskritimą taisyklingąjį p - kampį, tai pagal Pagrindinę brėžimo sąlygą ir Lemą 7.10 turime (p-1)/2 = 2^m , čia m - natūralusis skaičius, ir p = 2^m+1 + 1. Bet skaičius 2ⁿ + 1 yra pirminis, jeigu n yra 2 laipsnis, nes priešingai skaičius n turėtų nelyginį d, t.y.  n = d × s, ir tada skaičius 2ⁿ + 1 nebūtų pirminis:

Taigi   su natūraliuoju r.

Įrodyta.

Ferma manė, kad skaičiai  yra pirminiai su visais natūraliaisiais n ir paskelbė, kad patikrino, kai n £ 5. Iš čia visi pirminiai skaičiai, turintys pavidalą , vadinami Ferma pirminiais skaičiais. Kai n = 0; 1; 2; 3;4 skaičiai p = 3, 5, 17, 257, 65537 tikrai yra pirminiai. Bet 1732 m. L.Oileris (L.Euler,1707-1783) nustatė, kad skaičius 

yra sudėtinis. Iki šiol nėra žinoma daugiau pirminių Ferma skaičių. Pastebėsime, kad Teiginys 7.11 nusako tik būtinas taisyklingojo p -  kampio brėžimo sąlygas. Brėžti taisyklingąjį trikampį galima, nes cos(2p/3) = cos120° = -1/2. Galima brėžti ir taisyklingąjį 5 - kampį, nes cos(2p/5) = cos72° =

(Ö5-1)/4. 1801 metais 18-metis K. F. Gausas ( K.F.Gauss, 1777-1855) parodė, kad cos(2p/17) =

ir tuo pačiu, kad galima brėžti taisyklingąjį 17 - kampį. Gausas įrodė dar

daugiau: į apskritimą galima įbrėžti taisyklingąjį n - kampį tada ir tik tada, kada

skaičiaus n kanoninis skaidinys yra n = 2^k × p × × × q , čia k = 0, 1, 2, ..., o p, ..., q

yra pirminiai Ferma skaičiai.

Norint mums pakartoti Gauso rezultatą, reiktų įrodyti teiginį atvirkščią Teiginiui 7.11.

Teiginys 7.12 Jeigu p = 2^k +1 yra pirminis skaičius, tai į apskritimą galima

įbrėžti taisyklingąjį p - kampį.

Įrodymas. Mes jau žinome, kad užtenka parodyti, kad galima nubrėžti skaičių cos(2p/p). Skaičius cos(2p/p) Ī Q(cos(2p/p)) Ģ Q(e^2pi/p), ir pagal Teoremą 6.7

kūnas Q(e^2pi/p)  yra Galua kūnas virš Q, nes jis yra neredukuojamo virš Q polinomo x^p-1 + x^p-2 + × × × + x + 1 skaidinio kūnas. Tegu s Ī Gal(Q(e^2pi/p) / Q). Tada s (e^2pi/p) = e^2pi/p×m, su apibrėžtu m, 1 £ m £ p - 1. Iš čia funkcija s ® m

apibrėžia grupių izomorfizmą Gal(Q(e^2pi/p) / Q) ® (Z / pZ)^x . Taigi Galua plėtinio

Q(e^2pi/p) / Q Galua grupė G yra izomorfiška baigtinio kūno GF(p) multiplikacinei

grupei (Z / pZ)^x, kurios eilė yra lygi p - 1 = 2^k. Gavome, kad G yra p - grupė.

Iš Silovo Teoremos 4.4 (1), kai p = 2. žinome, kad egzistuoja tokia grupės G

pogrupių grandinė

(1)   = G₀ Ģ G₁ Ģ G₂ Ģ × × × Ģ G_k-1 Ģ G_k = G,

kad faktorgrupės G_i+1 / G_i su visais 0 £ i £ k - 1 eilė lygi 2. Šią pogrupių

grandinė atitinka kūno Q(e^2pi/p) pokūnių grandinė

(1)   ¢ = G¢₀ = Q(e^2pi/p) É G¢₁ É G¢₂ É × × × É G¢_k-1 É G¢_k = G¢ = Q,

ir [G_i : G_i+1] = 2 su visais 0 £ i £ k - 1: Jeigu u_i Ī G_i ir u_i Ļ G_i+1 ir

polinomas x² + b_ix + c_i , čia b_i, c_i Ī G_i+1; yra minimalusis u_i polinomas, tai

Tegu dabar a_i+1 = b²_i - 4c_i Ī G_i+1. Tada

ir a_k Ī Q. Įrodymui baigti belieka pasinaudoti Pagrindine brėžimo teorema (Teorema 7.4).

Įrodyta.