KŪNŲ TEORIJA
RIMANTAS GRIGUTIS
Praeitame skyriuje mes matėme, kad baigtinio matavimo Galua plėtinys yra separabilusis ir normalusis plėtinys (Išvada 5.6). Dabar įrodysime, kad teisingas ir atvirkščias teiginys.
Visų pirma mes įsitikinsime tuo, kad ne visi neredukuojami polinomai yra separabilieji. Pradėsime apibrėžimu.
Apibrėžimas 6.1 Tegu K yra kūnas. Mažiausias kūno K pokūnis vadinamas pirminiu K pokūniu. Jeigu pirminio K pokūnio elementų skaičius yra pirminis skaičius p, tai sakome, kad kūno K charakteristika yra lygi p, o jeigu pirminiame K pokūnyje yra begalinis elementų skaičius, tai sakome, kad kūno K charakteristika yra lygi nuliui.
Pastebėsime, kad kūno K pirminis pokūnis yra izomorfinis arba baigtiniam kūnui GF(p), jeigu kūno K charakteristika yra lygi pirminiam skaičiui p; arba racionaliųjų skaičių kūnui Q, jeigu kūno K charakteristika yra lygi 0. Jeigu kūno K charakteristika yra p, tai 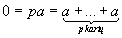 su visais a
su visais a 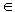 K. Kita kūno K, kurio charakteristika yra p, aritmetikos ypatybė pasireiškia lygybėje (a + b)p = ap + bp su visais a,b
K. Kita kūno K, kurio charakteristika yra p, aritmetikos ypatybė pasireiškia lygybėje (a + b)p = ap + bp su visais a,b 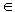 K, nes visi binominiai koeficientai išskyrus pirmąjį ir paskutinįjį dalijasi iš p. (Dėl tos pačios priežasties yra teisinga ir lygybė
K, nes visi binominiai koeficientai išskyrus pirmąjį ir paskutinįjį dalijasi iš p. (Dėl tos pačios priežasties yra teisinga ir lygybė 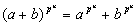 su visais a,b
su visais a,b 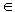 K ir n
K ir n 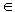 N). Iš čia turime, kad virš kūno K, kurio charakteristika yra p, polinomas xp + 1 = (x + 1)p nėra neredukuojamas.
N). Iš čia turime, kad virš kūno K, kurio charakteristika yra p, polinomas xp + 1 = (x + 1)p nėra neredukuojamas.
Apibrėžimas 6.2 Tegu f 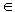 K[x],
K[x], 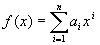 . Polinomo f (x) išvestine f ' (x) vadiname polinomą
. Polinomo f (x) išvestine f ' (x) vadiname polinomą
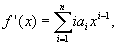
čia 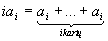
Šis išvestinės apibrėžimas realiems polinomams sutampa su įprastu išvestinės apibrėžimu, naudojančiu ribos savoką. Bet baigtiniuose kūnuose ribos savokos nėra, todėl prireikė formalaus išvestinės apibrėžimo. Tai leidžia suformuluoti polinomo separabilumo sąlygą.
Teiginys 6.3 Tegu f (x) yra neredukuojamas polinomas virš kūno K. Tada šios 4 sąlygos yra ekvivalenčios:
(1) polinomas f turi nors vieną kartotinę šaknį (skaidinio kūne);
(2) BBD( f,f' )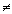 1;
1;
(3) kūno K charakteristika p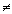 0 ir f (x) = g (xp), čia g (x)
0 ir f (x) = g (xp), čia g (x)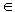 K[x];
K[x];
(4) visos polinomo šaknys yra kartotinės.
Įrodymas. Tegu F yra polinomo f skaidymo kūnas.
(1) Þ(2). Tegu r yra polinomo f (x) kartotinė šaknis: f (x) = (x - r)2g (x), čia g (x)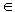 F[x] Tada viena išvestinės f ' (x) = 2(x - r)g (x) + (x - r)2g ' (x) = (x - r)(2g (x) + (x - r)g ' (x)) šaknimi yra r : f '(r) = 0 ir todėl BBD( f,f' )
F[x] Tada viena išvestinės f ' (x) = 2(x - r)g (x) + (x - r)2g ' (x) = (x - r)(2g (x) + (x - r)g ' (x)) šaknimi yra r : f '(r) = 0 ir todėl BBD( f,f' )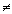 1.
1.
(2) Þ (3). Kadangi f yra neredukuojamas polinomas, o deg(f ') < deg(f ) ir BBD( f,f' )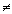 1, tai f ')
1, tai f ') 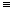 0. Bet tai neįmanoma virš nulinės charakteristikos kūno, todėl char K = p > 0 ir todėl
0. Bet tai neįmanoma virš nulinės charakteristikos kūno, todėl char K = p > 0 ir todėl 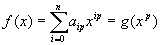 , čia g
, čia g 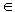 K[x].
K[x].
(3) Þ (4). Tegu f (x) = g (xp) ir tegu 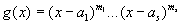 kūne F. Tada
kūne F. Tada 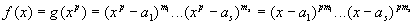 ,čia aip = ai, char F = p. Gavome, kad kiekvienos polinomo f šaknies kartotinumas nemažesnis už p.
,čia aip = ai, char F = p. Gavome, kad kiekvienos polinomo f šaknies kartotinumas nemažesnis už p.
(4)Þ(1). Akivaizdu (aš tikiuosi).
Įrodyta.
Išvada 6.4 Neredukuojamas polinomas virš kūno, kurio charakteristika yra lygi 0, yra separabilus.
Paskutinioji išvada mums sako, kad polinomo virš nulinės charakteristikos kūno skaidinio kūnas yra Galua plėtinys. Tai teisinga ir polinomams virš baigtinių kūnų (žr.: C. Paskaita apie neredukuojamus polinomus virš baigtinių kūnų). Tačiau tai nėra teisinga begaliniams kūnams, kurių charakteristika yra lygi p.
Pavyzdys. Tegu kūno K charakteristika yra lygi p (pavyzdžiui, GF(p)) ir tegu u yra transcendentinis elementas virš K. Tada racionaliųjų funkcijų kūno K (u) charakteristika yra lygi p ir polinomas xp - u yra neredukuojamas žiede K (u)[x], bet xp - u = (x - r)p virš polinomo xp - u skaidinio kūno, čia r - polinomo šaknis. Gavome, kad neredukuojamas polinomas gali turėti kartotines šaknis, tiesa, tik virš begalinių baigtinės charakteristikos kūnų.
Grįžkime prie Išvados 5.6 atvikščio teiginio įrodymo. Iš pradžių pastebėsime, kad kiekvienas kūnų izomorfizmas 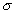 : K
: K 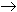 L generuoja žiedų izomorfizmą
L generuoja žiedų izomorfizmą 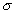 x : K[x]
x : K[x] 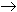 L[x], čia
L[x], čia 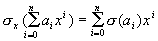 (skaitytojui paliekame įrodyti, kad tai yra žiedų izomorfizmas).
(skaitytojui paliekame įrodyti, kad tai yra žiedų izomorfizmas).
Teorema 6.6 Tegu 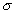 : K
: K 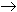 L yra kūnų izomorfizmas ir tegu
L yra kūnų izomorfizmas ir tegu 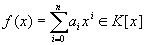 yra separabilus nojo laipsnio polinomas (n > 0). Jeigu F yra polinomo f skaidinio kūnas virš K, o E yra polinomo
yra separabilus nojo laipsnio polinomas (n > 0). Jeigu F yra polinomo f skaidinio kūnas virš K, o E yra polinomo 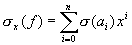 skaidinio kūnas virš L, tai egzistuoja lygiai [F : K] izomorfizmą generuojančių izomorfizmų
skaidinio kūnas virš L, tai egzistuoja lygiai [F : K] izomorfizmą generuojančių izomorfizmų 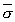 : F
: F 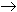 E (izomorfizmas
E (izomorfizmas 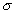 generuoja izomorfizmą
generuoja izomorfizmą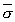 , jeigu
, jeigu 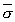 (a) =
(a) = 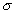 (a) su visais a
(a) su visais a 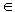 K).
K).
Įrodymas. Įrodysime indukcija pagal m = [F : K]. Jeigu m = 1, tai F = K ir todėl polinomo f skaidinio kūnu yra K, o polinomo 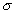 x(f ) skaidinio kūnu yra L, taigi, E = L. Turime, kad tada
x(f ) skaidinio kūnu yra L, taigi, E = L. Turime, kad tada 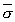 =
= 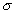 . Tegu dabar teorema yra teisinga su visais kūnais K ir visais polinomais h (x)
. Tegu dabar teorema yra teisinga su visais kūnais K ir visais polinomais h (x)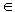 K[x], kurių skaidinio kūno laipsnis virš K yra mažesnis už m. Tegu [F : K] = m > 1 ir g yra polinomo f neredaguojamas daugiklis, kurio laipsnis yra d > 1. Polinomas
K[x], kurių skaidinio kūno laipsnis virš K yra mažesnis už m. Tegu [F : K] = m > 1 ir g yra polinomo f neredaguojamas daugiklis, kurio laipsnis yra d > 1. Polinomas 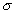 x(g ) yra neredukuojamas virš L, nes
x(g ) yra neredukuojamas virš L, nes 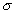 x yra izomorfizmas. Mes galime apibrėžti žiedų homomorfizmų kompoziciją
x yra izomorfizmas. Mes galime apibrėžti žiedų homomorfizmų kompoziciją
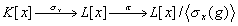
kurios branduolys 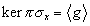 . Tegu u
. Tegu u 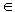 F yra polinomo g šaknis, o v
F yra polinomo g šaknis, o v 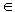 E kuri nors polinomo
E kuri nors polinomo 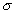 x(g ) šaknis. Parašykime homomorfizmų teoremą žiedams diagrama
x(g ) šaknis. Parašykime homomorfizmų teoremą žiedams diagrama
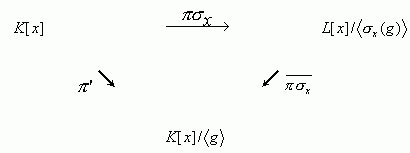
čia 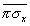 kūnų izomorfizmas. tada pagal Teoremą 1.5 turime
kūnų izomorfizmas. tada pagal Teoremą 1.5 turime
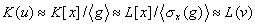
Tegu v1, ..., vd yra visos polinomo 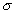 x(g ) šaknys. Tada pagal Teoremą 1.6 egzistuoja lygiai d tokių kūnų izomorfizmų
x(g ) šaknys. Tada pagal Teoremą 1.6 egzistuoja lygiai d tokių kūnų izomorfizmų 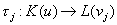 ; kad
; kad 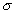 generuoja
generuoja 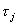 ir
ir 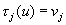 . Iš Teoremos 1.5 turime, kad [K (u) : K] = d > 1. Tada pagal Teoremą 1.8 gauname, kad
. Iš Teoremos 1.5 turime, kad [K (u) : K] = d > 1. Tada pagal Teoremą 1.8 gauname, kad 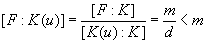 . Turime, kad kūnas F yra polinomo f skaidinio kūnas virš K [u] ir su visais
. Turime, kad kūnas F yra polinomo f skaidinio kūnas virš K [u] ir su visais 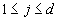 kūnas E yra polinomo
kūnas E yra polinomo 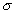 x(f ) skaidinio kūnas virš L (vj). Pagal indukcijos prielaidą turime, kad su visais
x(f ) skaidinio kūnas virš L (vj). Pagal indukcijos prielaidą turime, kad su visais 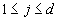 egzistuoja lygiai
egzistuoja lygiai 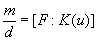 izomorfizmų w : F
izomorfizmų w : F E, kuriuos generuoja
E, kuriuos generuoja 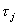 . Iš čia turime, kad egzistuoja lygiai
. Iš čia turime, kad egzistuoja lygiai 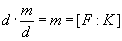 izomorfizmų, kuriuos generuoja
izomorfizmų, kuriuos generuoja 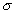
Įrodyta.
Dabar įrodysime norimą teoremą.
Teorema 6.7. Tegu F / K yra kūno plėtinys. Tada teiginiai yra ekvivalentūs:
(1) F / K yra baigtinis Galua plėtinys.
(2) F / K yra baigtinis, normalusis, separabilusis plėtinys.
(3) F yra separabilaus polinomo skaidinio kūnas virš K
Įrodymas. (1) 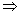 (2) : tai Išvada 5.6.
(2) : tai Išvada 5.6.
(2)Þ(3) : Tegu {v1, ..., vn} yra kūno F bazė virš K (plėtinys F / K yra baigtinis). Tegu fi 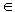 K[x] yra minimalusis vi polinomas virš K, _ čia
K[x] yra minimalusis vi polinomas virš K, _ čia 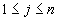 . Plėtinys F / K yra separabilusis, todėl visi fi yra separabilūs virš K. Plėtinys F / Kyra normalusis, todėl F yra separabilaus polinomo f = fi ... fn skaidinio kūnas, nes visos polinomų fi> šaknys, o taip pat ir polinomo f šaknys, yra kūne F.
. Plėtinys F / K yra separabilusis, todėl visi fi yra separabilūs virš K. Plėtinys F / Kyra normalusis, todėl F yra separabilaus polinomo f = fi ... fn skaidinio kūnas, nes visos polinomų fi> šaknys, o taip pat ir polinomo f šaknys, yra kūne F.
(3)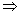 (1) : Tegu F yra separabilaus polinomo f
(1) : Tegu F yra separabilaus polinomo f 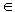 K [x] skaidinio kūnu. Tegu G = Gal(F / K). Tada G = Gal(F / K"), nes F yra taip pat ir polinomo f, kaip polinomo virš K", skaidinio kūnas. Tada pagal Teoremą 6.6 turime
K [x] skaidinio kūnu. Tegu G = Gal(F / K). Tada G = Gal(F / K"), nes F yra taip pat ir polinomo f, kaip polinomo virš K", skaidinio kūnas. Tada pagal Teoremą 6.6 turime
[F : K] = |Gal(F / K)| = |Gal(F / K")|= [F : K"].
Gavome, kad K = K" ir todėl F / Kyra baigtinis Galua plėtinys.
Įrodyta.
Taigi, nuo šiol į baigtinį Galua plėtinį galima žiūrėti kaip į separabilaus polinomo skaidinio kūną.
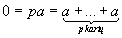 su visais a
su visais a 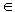 K. Kita kūno K, kurio charakteristika yra p, aritmetikos ypatybė pasireiškia lygybėje (a + b)p = ap + bp su visais a,b
K. Kita kūno K, kurio charakteristika yra p, aritmetikos ypatybė pasireiškia lygybėje (a + b)p = ap + bp su visais a,b 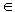 K, nes visi binominiai koeficientai išskyrus pirmąjį ir paskutinįjį dalijasi iš p. (Dėl tos pačios priežasties yra teisinga ir lygybė
K, nes visi binominiai koeficientai išskyrus pirmąjį ir paskutinįjį dalijasi iš p. (Dėl tos pačios priežasties yra teisinga ir lygybė 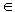 K ir n
K ir n 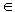 N). Iš čia turime, kad virš kūno K, kurio charakteristika yra p, polinomas xp + 1 = (x + 1)p nėra neredukuojamas.
N). Iš čia turime, kad virš kūno K, kurio charakteristika yra p, polinomas xp + 1 = (x + 1)p nėra neredukuojamas.
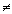 1;
1;
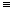 0. Bet tai neįmanoma virš nulinės charakteristikos kūno, todėl char K = p > 0 ir todėl
0. Bet tai neįmanoma virš nulinės charakteristikos kūno, todėl char K = p > 0 ir todėl 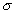 : K
: K 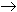 L generuoja žiedų izomorfizmą
L generuoja žiedų izomorfizmą 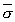 : F
: F 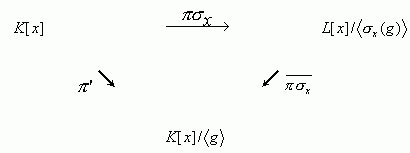
 (1) : Tegu F yra separabilaus polinomo f
(1) : Tegu F yra separabilaus polinomo f