NEREDUKUOJAMI POLINOMAI VIRŠ BAIGTINIŲ KŪNŲ

Rimantas GRIGUTIS

Neredukuojami polinomai baigtinių kūnų teorijoje vaidina panašų vaidmenį kaip ir pirminiai skaičiai skaičių teorijoje. Dauguma konstruktyvių uždavinių sprendimų remiasi neredukuojamų polinomų savybėmis. Štai keletas iš jų:

1. Neredukuojamas virš GF(q) polinomas f(x) yra savo šaknies a minimalusis polinomas, I = {g(x) Î GF(q) [x] | g(a) = 0} = (f(x)), t.y. a yra polinomo g(x) Î GF(q) [x] šaknis tada ir tik tada, kai g(x) dalijasi iš f(x).

2. Bet kuriam natūraliajam skaičiui n virš bet kokio baigtinio kūno GF(q) egzistuoja neredukuojamas n-ojo laipsnio polinomas.

Dabar nustatysime kitas neredukuojamų polinomų savybes.

1 teiginys. Tegu f(x) Î GF(q) [x] yra neredukuojamas n-ojo laipsnio polinomas, o a - viena iš polinomo f(x) šaknų, esanti kūno GF(q) plėtinyje. Tada polinomo f(x) skaidinio kūnas K yra (GF(q))(a) = GF(qⁿ).

Įrodymas. Iš apibrėžimo žinome, kad polinomo f(x) skaidinio kūnas yra mažiausias kūno GF(q) plėtinys, kuriame yra visos polinomo f(x) šaknys. Todėl

GF(q) Í (GF(q))(a) Í K.

Kita vertus, [(GF(q))(a) : GF(q)] = n ir |(GF(q))(a)| = qⁿ. Žinodami , kad visi kūno (GF(q))( a) elementai yra polinomo šaknys. Taigi ir, todėl dalijasi iš f(x): visos polinomo f(x) šaknys yra ir polinomo šaknys.

Todėl

K Í (GF(q))( a)

ir

K = (GF(q))(a) = GF(qⁿ).

2 teiginys. Tegu f(x) Î GF(q) [x] neredukuojamas n-ojo laipsnio polinomas. Tada polinomas dalijasi iš f(x) tada ir tik tada, kai m dalijasi iš n.

Įrodymas. Jau žinome, kad polinomo f(x) skaidinio kūnas yra GF(qⁿ), o polinomo skaidinio kūnas yra GF(q^m). Be to, jei kūnas GF(qⁿ) yra kūno GF(q^m) pokūnis, GF(qⁿ) Ì GF(q^m), tai m dalijasi iš n.

Tegu dalijasi iš f(x). Tada visos polinomo f(x) šaknys yra ir polinomo šaknys. Todėl GF(qⁿ) Ì GF(q^m) ir m dalijasi iš n.

Priešingai, tegu m dalijasi iš n. Tada GF(qⁿ) Ì GF(q^m) ir visos polinomo f(x) šaknys priklauso kūnui GF(q^m). Bet kūno GF(q^m) elementai - tai polinomo šaknys ir todėl polinomo f(x) šaknis a yra polinomo šaknis. Taigi dalijasi iš f(x).

Neredukuojamų polinomų virš baigtinių kūnų šaknys reiškiamos paprastai.

3 teiginys. Tegu f(x) Î GF(q) [x] yra n-ojo laipsnio neredukuojamas polinomas ir a - kuri nors polinomo f(x) šaknis polinomo skaidinio kūne GF(qⁿ). Tada kūno GF(qⁿ) elementai

yra visos skirtingos polinomo f(x) šaknys ir n yra mažiausias natūralusis skaičius, kuriam teisinga lygybė .

Įrodymas. Tegu f(x) = a₀+ a₁x + … + a_nxⁿ, a_i Î GF(q), 0 <= i <= n, o a – polinomo f(x) šaknis polinomo skaidinio kūne GF(qⁿ):

f(a) = a₀ + a₁a + … + a_naⁿ = 0.

Kūno GF(qⁿ) charakteristika yra pirminis skaičius p, o q yra p laipsnis. Todėl a_i^q = a_i ir

f(a^q) = a₀ + a₁a^q + …+ a_na^qn = a₀^q + a₁^qa^q + … + a_n^qa^qn

= a₀^q + (a₁a)^q + … + (a_naⁿ) ^q = (a₀ + a₁a + … + a_naⁿ) ^q

= (f(a))^q = 0.

Taigi, jeigu a yra polinomo f(x) šaknis, tai ir a^q yra šio polinomo šaknis, taip pat šaknys yra ir elementai

Visi šioje sekoje esantys elementai yra skirtingi, nes, jeigu , 0 <= i < j <= n - 1, tai

t.y. a būtų polinomo šaknis ir tada polinomas dalytųsi iš f(x), ir n + i - j dalytųsi iš n. Bet tai prieštarauja nelygybėms 0 < n+ i - j < n.

4 išvada. Tegu f(x) Î GF(q) [x] yra n-jo laipsnio neredukuojamas polinomas ir - šio polinomo šaknys kūne GF(qⁿ). Tada šių šaknų eilės kūno GF(qⁿ) multiplikacinėje grupėje GF(qⁿ)* yra lygios:

Įrodymas. Grupė GF(qⁿ)* yra (qⁿ - 1)-osios eilės ciklinė grupė, todėl elemento a eilė šioje grupėje yra qⁿ - 1 daliklis:

Tada

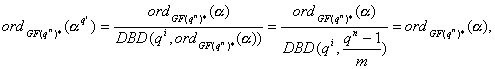
, 0 <= i <= n – 1,

nes q = p^s, p = charGF(q) ir