Tensor-border surfaces
Kestutis Karciauskas
Multisided tensor-border surfaces (term due to J. Peters) are generalizations of quadrangular Bézier patches and were introduced by M. Sabin and Hosaka-Kimura. Spline surfaces of any complex topology can be constructed easily using tensor-border patches.
Here you can see some simple but essential examples. Our software does not
allow us to display spline surfaces built from remarkably greater number of Bézier patches
in a real time.
Boundary curves of a tensor-border patch are Bézier curves with the same family of tangent planes as a tensor product surface. This property enables us to use the same smooth joining
conditions as for quadrangular Bézier patches.
Here we briefly describe some of the most simple and widely used conditions.
Smooth joining of quadrangular Bézier patches
For a simplicity let us consider only smoothness of the first order.
Suppose Bézier surfaces F and G are defined via control
points Pij, i=0,...,n, j=0,...,m, and Qij, i=0,...,n, j=0,...,k. Let their common
boundary Bézier curve C has control points P0m=Q00, P1m=Q10,...,
Pnm=Qn0.
Any kind of the first order smoothness conditions involves only control
points of the common boundary curve and the next layer of control points
of both surfaces F and G. It means that smooth joining of
F and G depends only of the points Pij,
i=0,...,n, j=m-1,m, and Qi1,
i=0,...,n.
If the surfaces are rational then their smoothness also depends of the weights
of corresponding control points.
Parametric smoothness
Suppose the patch F is defined over square 0< u < 1,
0< v < 1, and the patch G is defined over the adjacent
square 0< u < 1, 1< v < 2.
Hence their common boundary curve C corresponds to the parameter value
v=1. The most simple case of smooth joining occur, when the derivatives of
parametric curves coincide along the curve C:u=const of both surfaces,
e.g. F'v|v=1=G'v|v=1.
Here is the classical sufficient condition of parametric smoothness
Pim = (Pi,m-1 + Qi1) / 2,
i=0,..., n.
(1)
If the surfaces F and G are rational then any control point
R with a corresponding weight w is replaced by a homogeneous
point R=(wR,w) with four coordinates. In this case a
traditional smoothness condition has the following form
Pim = (Pi,m-1 + Qi1) / 2,
i=0,..., n.
(2)
If the adjacent squares are replaced by adjacent rectangulars with a ratio of
there edges in v direction µ0 : µ1
then condition (1) is modified as follows
Pim=(µ1Pi,m1 + µ0Qi1)/
(µ0 + µ1), i=0,...,n.
(3)
Similarly the condition (2) is replaced by
Pim = (µ1 Pi,m-1+
µ0 Qi1)/(µ0 +µ1),
i=0,...,n.
(4)
The last condition (4) is a geometric smoothness for (bi)order(3,3) NURBS
surfaces.
It is convinient to consider seperately the affine combinations of control
points and their weights. Let the weights of control points of the surfaces F and
G are denoted by wij and wij respectively.
It is also assumed that
w0m = w00,
w1m = w10, ...,
wnm = wn0.
Parts of spline surfaces are constructed using following smoothness
condition:
-
the control points satisfy formula (1);
-
wi,m-1 = wi1 = W wim, where W
has any positive value.
Geometric smoothness
Parametric smoothness is used when spline surface is built from quadrangular patches and
their "inner" corner points belong exactly to four patches. So one can model only topologicaly
deformed square, cilinder and torus. More general geometric smoothness conditions for
multisided patches
allow us to build spline surfaces of any topology.
Spline surfaces due to J. Peters are good examples of such approach.
By a defintion two quadrangular Bézier patches F and G
are geometric smooth along common boundary Bézier curve
C, if their tangent planes coincide at any point on it.
Let Bézier patches F ir G are defined over adjacent squares,
as we considered above. We denote
Fu=F'u|
v=1=G'u|v=1,
Fv = F'v|v=1,
Gv = G'v|v=1.
Geometric smoothness means that vectors Fu, Fv
and Gv are complanar for any value
0 < u < 1.
Though there are various forms of necessary and sufficient
conditions of geometric smoothness it is not convenient to use them
in practice. Better approach is to discover some sufficient conditions
that fit naturally to a handled situation. Corresponding formulas are
more complicated then (1)-(4) so we do not present them here.
Tensor-border net and patch
A multisided tensor-border net of order n is composed using the following
combinatorial scheme: boundary points are control points of m
Bézier curves of degree n, and the layer adjacent to every boundary
curve is the same as that of a Bézier patch of bidegree (n,n).
By a definition a tensor-border patch has the same family of tangent planes
along each boundary Bézier curve as
the corresponding tensor product surface with the same adjacent two layers of
control points and weights.
A tensor-border net of order two is the Sabin net, and if it has order three then
we obtain the Hosaka-Kimura net. Note that the same tensor-border net
can be used for different tensor-border patches.
There are two main types of these patches:
a multisided piece on an algebraic surface and a patche built using
smoothly joined quadrangular Bézier patches.
Shape quality of the first type patches are better but the degree of parametrization
is higher.
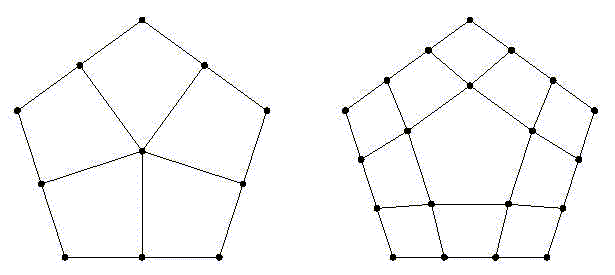
Sabin and Hosaka-Kimura pentagonal nets.
A designer who works with Bézier patches does not need to know
matematical formulas that define them. It is enough to feel the influence
of control points and weights to the form of the surface. The same we can say about
tensor-border patches, which have even more complicated mathematical background.
Spline surfaces
Spline surfaces of arbitrary topology are constructed using any polyhedral mesh of
control points. At first a step of Cattmull-Clark or Doo-Sabin polyhedra subdivision
algorithm is applied. New polyhedra contains only quadrangular (Cattmull-Clark) faces
or every vertex belongs to exactly four faces (Doo-Sabin). Then we build a complex of
multisided tensor-border nets that satisfy the mentioned smoothness conditions along
each boundary.
For example, if all faces are quadrangular then any subdivision step is not
needed and Sabin nets are constructed via the following simple procedure:
- the inner net point coinsides with the vertex of the mesh;
- corner points of the net are centroids of the faces adjacent to
the fixed vertex;
- the inner points of the net border are middle points of the
edges adjacent to the fixed vertex.
The obtained Sabin nets satisfy the condition (1).
Some other modifications use different smoothness conditions.
Back to FFSMS

