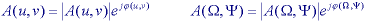
There are a variety of properties associated with the Fourier transform and the inverse Fourier transform. The following are some of the most relevant for digital image processing.
* The Fourier transform is, in general, a complex function of the real frequency variables. As such the transform can be written in terms of its magnitude and phase.
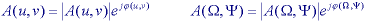
* A 2D signal can also be complex and thus written in terms of its magnitude and phase.
* If a 2D signal is real, then the Fourier transform has certain symmetries.
The symbol (*) indicates complex conjugation. For real signals eq. leads directly to:
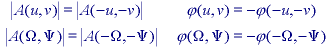
* If a 2D signal is real and even, then the Fourier transform is real and even.
* The Fourier and the inverse Fourier transforms are linear operations.
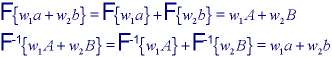
where a and b are 2D signals (images) and w1 and w2 are arbitrary, complex constants.
* The Fourier transform in discrete space,
A(
,
), is periodic in both
and . Both periods are 2
.
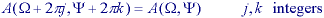
* The energy, E, in a signal can be measured either in the spatial domain or the frequency domain. For a signal with finite energy:
Parseval's theorem (2D continuous space):
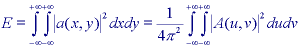
Parseval's theorem (2D discrete space):
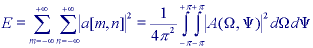
This "signal energy" is not to be confused with the physical energy in the phenomenon that produced the signal. If, for example, the value a[m,n] represents a photon count, then the physical energy is proportional to the amplitude, a, and not the square of the amplitude. This is generally the case in video imaging.
* Given three, multi-dimensional signals a, b, and c and their Fourier transforms A, B, and C:
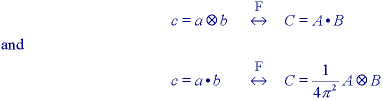
In words, convolution in the spatial domain is equivalent to multiplication in the Fourier (frequency) domain and vice-versa. This is a central result which provides not only a methodology for the implementation of a convolution but also insight into how two signals interact with each other--under convolution--to produce a third signal. We shall make extensive use of this result later.
* If a two-dimensional signal a(x,y) is scaled in its spatial coordinates then:
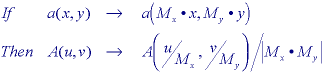
* If a two-dimensional signal a(x,y) has Fourier spectrum A(u,v) then:
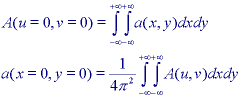
* If a two-dimensional signal a(x,y) has Fourier spectrum A(u,v) then:
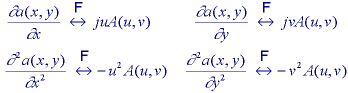
,)|), and Figure 4c the phase
(,).
,)|)
(,)
Both the magnitude and the phase functions are necessary for the complete reconstruction of an image from its Fourier transform. Figure 5a shows what happens when Figure 4a is restored solely on the basis of the magnitude information and Figure 5b shows what happens when Figure 4a is restored solely on the basis of the phase information.
Figure 5a Figure 5b
(,) = 0
|A(,)| = constant
Neither the magnitude information nor the phase information is sufficient to restore the image. The magnitude-only image (Figure 5a) is unrecognizable and has severe dynamic range problems. The phase-only image (Figure 5b) is barely recognizable, that is, severely degraded in quality.
). When the 2D
signal exhibits a circular symmetry this means that:
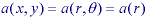
where r2 = x2 + y2 and
tan = y/x. As a number of physical systems
such as lenses exhibit circular symmetry, it is useful to be able to compute an
appropriate Fourier representation.
The Fourier transform A(u, v) can be written in polar coordinates
A(
r,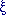
) and
then, for a circularly symmetric signal, rewritten as a ankel
transform:
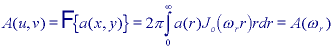
where
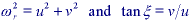and Jo(*) is a Bessel function of the first kind of order
zero.
The inverse ankel transform is given by:
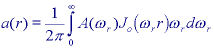
The Fourier transform of a circularly symmetric 2D signal is a function of only
the radial frequency, r. The
dependence on the angular frequency, 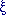, has vanished.
Further, if a(x,y) = a(r) is real, then it
is automatically even due to the circular symmetry. According to equation ,
A(r) will then be real and even.