Mathematics-based Operations

• Binary operations
• Arithmetic-based operations

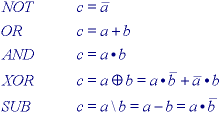
We distinguish in this section between binary arithmetic and ordinary arithmetic. In the binary case there are two brightness values "0" and "1". In the ordinary case we begin with 2^B brightness values or levels but the processing of the image can easily generate many more levels. For this reason many software systems provide 16 or 32 bit representations for pixel brightnesses in order to avoid problems with arithmetic overflow.

Binary operations

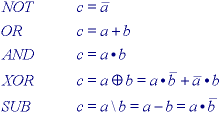
The implication is that each operation is applied on a pixel-by-pixel basis. For example, 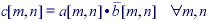. The definition of each operation is:

These operations are illustrated in Figure 22 where the binary value "1" is shown in black and the value "0" in white.

a) Image a b) Image b

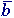c) NOT(b) = d) OR(a,b) = a + b e) AND(a,b) = a * b

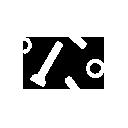f) XOR(a,b) = a b g) SUB(a,b) = a \ b

Figure 22: Examples of the various binary point operations.

The SUB(*) operation can be particularly useful when the image a represents a region-of-interest that we want to analyze systematically and the image b represents objects that, having been analyzed, can now be discarded, that is subtracted, from the region.

Arithmetic-based operations