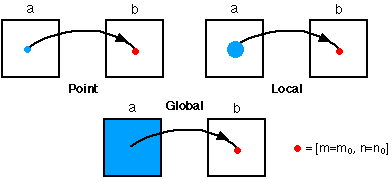
Figure 2: Illustration of various types of image operations








There is a variety of ways to classify and characterize image operations. The reason for doing so is to understand what type of results we might expect to achieve with a given type of operation or what might be the computational burden associated with a given operation.
Operation
|
Characterization
|
Generic
Complexity/Pixel
|
| *
Point
|
-
the output value at a specific coordinate is dependent only on the input value
at that same coordinate.
|
constant
|
| *
Local
|
-
the output value at a specific coordinate is dependent on the input values in
the neighborhood of that same coordinate.
|
P2
|
| *
Global
|
-
the output value at a specific coordinate is dependent on all the values in the
input image.
|
N2
|
This is shown graphically in Figure 2.

Figure 2: Illustration of various types of image operations
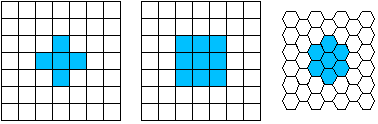
* Rectangular sampling - In most cases, images are sampled by laying a rectangular grid over an image as illustrated in Figure 1. This results in the type of sampling shown in Figure 3ab.
* exagonal sampling - An alternative sampling scheme is shown in Figure 3c and is termed hexagonal sampling.
Both sampling schemes have been studied extensively and both represent a possible periodic tiling of the continuous image space. We will restrict our attention, however, to only rectangular sampling as it remains, due to hardware and software considerations, the method of choice.
Local operations produce an output pixel value b[m=mo,n=no] based upon the pixel values in the neighborhood of a[m=mo,n=no]. Some of the most common neighborhoods are the 4-connected neighborhood and the 8-connected neighborhood in the case of rectangular sampling and the 6-connected neighborhood in the case of hexagonal sampling illustrated in Figure 3.