<< >> Up Title Contents Index

Contour Representations

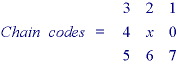
When dealing with a region or object, several compact representations are available that can facilitate manipulation of and measurements on the object. In each case we assume that we begin with an image representation of the object as shown in Figure 8a,b. Several techniques exist to represent the region or object by describing its contour.

Chain code

This representation is based upon the work of Freeman . We follow the contour in a clockwise manner and keep track of the directions as we go from one contour pixel to the next. For the standard implementation of the chain code we consider a contour pixel to be an object pixel that has a background (non-object) pixel as one or more of its 4-connected neighbors. See Figures 3a and 8c.

The codes associated with eight possible directions are the chain codes and, with x as the current contour pixel position, the codes are generally defined as:

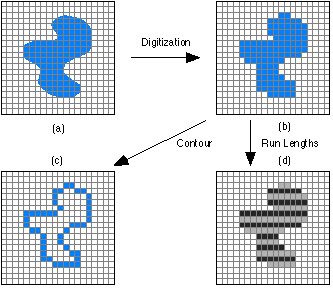
Figure 8: Region (shaded) as it is transformed from (a) continuous to (b) discrete form and then considered as a (c) contour or (d) run lengths illustrated in alternating colors.

Chain code properties

* Even codes {0,2,4,6} correspond to horizontal and vertical directions; odd codes {1,3,5,7} correspond to the diagonal directions.

* Each code can be considered as the angular direction, in multiples of 45deg., that we must move to go from one contour pixel to the next.

* The absolute coordinates [m,n] of the first contour pixel (e.g. top, leftmost) together with the chain code of the contour represent a complete description of the discrete region contour.

* When there is a change between two consecutive chain codes, then the contour has changed direction. This point is defined as a corner.

Crack code

An alternative to the chain code for contour encoding is to use neither the contour pixels associated with the object nor the contour pixels associated with background but rather the line, the "crack", in between. This is illustrated with an enlargement of a portion of Figure 8 in Figure 9.

The "crack" code can be viewed as a chain code with four possible directions instead of eight.

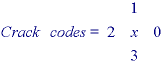
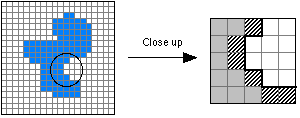
(a) (b)

Figure 9: (a) Object including part to be studied. (b) Contour pixels as used in the chain code are diagonally shaded. The "crack" is shown with the thick black line.

The chain code for the enlarged section of Figure 9b, from top to bottom, is {5,6,7,7,0}. The crack code is {3,2,3,3,0,3,0,0}.

Run codes

A third representation is based on coding the consecutive pixels along a row--a run--that belong to an object by giving the starting position of the run and the ending position of the run. Such runs are illustrated in Figure 8d. There are a number of alternatives for the precise definition of the positions. Which alternative should be used depends upon the application and thus will not be discussed here.

<< >> Up Title Contents Index