KOMPIUTERIJOS KATEDRA
Kursinių, bakalauro ir magistrinių darbų temos
2003-2004 mokslo metams
- trečio kurso studentai kaip kursinį darbą pasirinkti iki 2003 m. lapkričio 15 d.
- ketvirto kurso studentai kaip bakalauro darbą pasirinkti iki 2003 m. spalio 15 d.
- abiejų kursų magistrantai pasirinkti iki 2003 m. spalio 15 d.
Temos:
"Kalbos sintezė", vadovas - doc. A. Bastys
Pastaruoju metu sparčiai tobulėja kalbos sintezavimo sistemos. Sintezuojamos kalbos kokybė ženkliai priklauso nuo garsų jungimo kokybės. Šiame darbe siūloma pagvildenti lietuvių kalbos garsų jungimo problemą. Reikėtų realizuoti keletą skirtingų dvigarsių ir dvibalsių apjungimo algoritmų ir palyginti jų kokybę sintezuojant lietuvių kalbą. Sintezuojami garsų junginiai turėtų remtis kokiu nors kalbos modeliu ir iš anksto įrašytu etaloninių garsų rinkiniu. Studentai, pasirinkę šią temą, išmoks dirbti su paketu MATLAB, kuris idealiai tinka signalų analizei.
"Elektrokardiogramų kompiuterinė analizė", vadovas - doc. A. Bastys
Kompiuterinė medicininių signalų analizė atveria naujus horizontus pacientų susirgimų diagnozei. Šiame darbe siūloma atlikti kompiuterinę skaitmeninių elektrokardiogramų analizę. Pradiniame darbo etape reikėtų sukurti širdies ciklų (širdies susitraukimo ritmo) išskyrimo programą. Toliau reikėtų parinkti mažu parametrų skaičiumi aprašomą širdies ritmo modelį ir adaptuoti modelio parametrus prie paciento elektrokardiogramos įrašo. Galiniame darbo etape siūloma ištirti ritmo modelio parametrų informatyvumą širdies veiklos sutrikimų diagnozei. Čia pagrindinis programų paketas irgi būtų MATLAB.
"Transformacijos duomenų kompresijai", vadovas - doc. A. Bastys
Didėjant informacinių srautų galingumui duomenų glaudinimo problema išlieka daugelio tyrinėtojų dėmesio centre. Šiame darbe dėmesys akcentuojamas į vieno duomenų kompresijos schemos etapo, vadinamo transformacija, analizę. Siūloma palyginti diskrečiosios Furjė, kosinuso ir vilnelių transformacijų efektyvumą duomenų glaudinimui. Atskirai reikėtų ištirti vienmačių (garso, elektrokardiogramos) ir dvimačių (skenuoti paveiksliukai) duomenų tranformacijų kokybę. Kokybės kriterijumi galima paimti santykį paprastosios entropijos pradinių duomenų su ta pačia entropija transformuotų duomenų.
"Virtualioji fizikos laboratorija", vadovas - doc. A. Bastys
Dėl ekonominių ir edukologinių priežasčių vis daugiau atsiranda virtualiųjų fizikos laboratorijų (VFL). VFL Internete imituoja įvairius fizikinius reiškinius ir suteikia galimybę studentui savarankiškai namuose pasiruošti realiam darbui auditorijoje arba pilnai pakeičia laboratorinį darbą. Atliekant darbą reikėtų derinti žinias fizikos ir internetinių technologijų srityse. Darbas bus atliekamas bendradarbiaujant su VU fizikos fakulteto kolegomis. Pageidautinos bendros žinios apie HTML, Java, Java3D ir VRML programavimo priemones. Sveikintina iniciatyva, pavyzdžiui galite siūlyti analogiškus projektus mokyklose skaitomiems fizikos ar chemijos kursams.
"Biosignalų kompiuterinė analizė", vadovas - doc. A. Bastys
Medicininėse įstaigose plintant skaitmeninei biosignalų (elektrokardiogramų, elektroencefalogramų, kraujospūdžio ir pan.) registravimo aparatūrai atsiranda galimybė išryškinti žmogaus akimi sunkiai pastebimą informaciją. Šiame darbe numatomas bendradarbiavimas su Gamtos fakulteto biofizikos katedros signalų registravimo katedra. Pagrindinę darbo dalį sudarytų kraujospūdžio dinamikos nustatymas, remiantis netiesioginiais fotodetektorių parodymais. Darbo eigoje yra atliekami praktiniai eksperimentai , tai pat jūsų atlikti tyrimai bus naudojami medicininės aparatūros kūrime, vaistų testavime.
"Atsparių triukšmui ir transformacijoms vandens ženklų formavimas", vadovas - doc. A. Bastys
Vandens ženklais vadinami prie originalaus vaizdo ar garso signalo pridedami specifiniai mažos amplitudės signalai, kurie subjektyviai nepastebimi ir negirdimi, tačiau jie aptinkami vandens ženklų paieškos programomis. Šie ženklai yra naudojami apsaugoti duomenis nuo nelegalaus kopijavimo. Pradžiai darbe reikėtų įsisavinti klasikinius vandens ženklų kūrimo algoritmus. Pastebėta, kad tradiciniais algoritmais gauti vandens ženklai dingsta atlikus paprastas transformacijas, pvz. keičiant mastelį. Pagrindinis jūsų darbo tikslas sukurti atsparius elementarioms vaizdų ir garsų transformacijos vandens ženklų algoritmus.
"Didelių sveikųjų skaičių greita aritmetika", vadovas - doc. A. Bastys
Tradiciškai sveikajam skaičiui saugoti kompiuteryje skiriamas fiksuotas baitų skaičius. Tačiau pirminių skaičių paieškos, kodavimo, kompresijos, kriptografijos ir kiti algoritmai reikalauja dirbti su labai dideliais sveikaisiais skaičiais, kuriems tradiciškai kompiuteryje skiriamos vietos nepakanka. Šiame darbe siūloma įsisavinti naudojamus didelių sveikųjų skaičių greitos aritmetikos algoritmus, išsiaiškinti jų efektyvumą RSA ar pirminių skaičių paieškos algoritmų atveju.
"Universalieji kodai", vadovas - doc. A. Bastys
Universalieji kodai skirti koduoti bet kokio iš anksto nežinomo dydžio skaičius. Tradiciškai yra taikomi Elias arba Fibonačio universalieji kodai. Plačiau apie juos galima paskaityti http://www.mif.vu.lt/~bastys/ duomenų kompresijos skyrelyje. Šiame darbe siūloma išanalizuoti Elias ir Fibonačio tipo universaliųjų kokų efektyvumo priklausomybę nuo naudojamos skaičiavimo sistemos. Darbo tikslas surasti efektyvius universaliuosius kodus, kuriuos būtų galima praktiškai panaudoti duomenų kompresijos algoritmuose.
"Transporto srauto video vaizdų kompiuterinė analizė", vadovas - doc. A. Bastys
Pataruoju metu pasaulyje sparčiai vystomos specializuotos kompiuterinės atpažinimo sistemos. Šiame darbe siūloma realizuoti kompiuterinę transporto srauto video vaizdų analizės sistemą arba jos atskiras komponentes. Bene įdomiausi uždaviniai būtų kompiuteriniu algoritmu atpažinti judančius objektus (automobilius), įvertinti jų greitį ir atpažinti automobilio kategoriją ar numerį. Kadangi bendru atveju transporto srauto kompiuterinės analizės sistema yra sudėtinga ir imli programavimui, šį darbą gali pasirinkti atlikti kelių studentų grupelė, kurios nariai numatytų tarpusavyje atskirai kuriamų sistemos komponenčių apjungimą į bendrą sistemą.
"Diktoriaus atpažinimas arba verifikacija", vadovas - doc. A. Bastys
Diktoriaus atpažinimas arba verifikacija yra tradiciniai šnekamosios kalbos kompiuterinės analizės uždaviniai. Pirmuoju atveju reikia surasti iš anksto įrašytoje diktorių kalbos pavyzdžių bazėje labiausiai panašų įrašą į naujai pateiktą kalbos signalo fragmentą ir nuspręsti ar įrašai priklauso tam pačiam žmogui; antruoju atveju užduotis kiek paprastesnė - naujam kalbos įrašui pateikiamas konkretus diktorius ir reikia patvirtinti arba paneigti teiginį, kad šie įrašai priklauso tam pačiam diktoriui. Kokybiškas šio uždavinio sprendimas turėtų plačius taikymus kompiuterių interaktyvumo, apsaugos, telekomunikacijos ir kitose srityse.
"RSA šifravimo algoritmas ir kodo saugumas", vadovas - doc. A. Bastys
RSA (Rivest, Shamir ir Adleman) duomenų užšifravimo (kriptografijos) algoritmas ir jo modifikacijos yra plačiai taikomos kompiuterių duomenų apsaugos, bankų, telekomunikacijos ir kitose sistemose. Fiksuoto RSA kodo saugumas priklauso nuo sugebėjimo išskaidyti didelius natūraliuosius skaičius dauginamaisiais. Darbe siūloma realizuoti klasikinį RSA algoritmą bei išsiaiškinti kodo saugumą elipsinių kreivių ir kvadratinio rėčio algoritmais besiremiančių skaičių faktorizacijos algoritmų atžvilgiu bei pasiūlyti savo RSA modifikacijas, kurios padidintų šifravimo saugumą.
"Kvantiniai skaičiavimai", vadovas - doc. A. Bastys
Kvantiniai skaičiavimai nauja sparčiai besivystanti informatikos šaka. Kaip klasikinė fizika skiriasi nuo kvantinės, taip ir kvantiniai kompiuteriai iš esmės skiriasi nuo įprastų kompiuterių. Kadangi kvantiniai kompiuteriai dar tik kuriami, darbe teks apsiriboti tik literatūros studijomis ir klasikinių kvantiniais skaičiavimais pagrįstų algoritmų analize. Mokslinė-tiriamoji darbo dalis būtų atrasti naujas prasmingas kvantinių skaičiavimų taikymo sritis bei pasiūlyti atitinkamus kvantinius algoritmus.
"Nelegalios reklamos atpažinimas", vadovas - doc. A. Bastys
Taip vadinamas 25-asis kadras tapo nelegalios reklamos klasika. Jos esmė yra ta, kad į televizijos laidas, filmus, videojuostas yra įmontuojami pavieniai reklamos kadrai, kurie paprasta rega yra nepastebi, tačiau turi psichologinį poveikį į pasąmonę ir tokiu būdu, neatsiklausus žiūrovo, jam yra daromas poveikis. Darbo tikslas būtų atpažinti nelegalios reklamos kadrus pateiktame įraše ir realizuoti sistemą, kuri kompiuteriu priimamose TV programose ieškotų nematomų reklamos kadrų.
"Paviršių ir kreivių kolizijos", vadovas - doc. S.Zubė
Praktikoje geometriniai objektai yra užduodami įvairiomis algebrinėmis lygtimis. Gana dažnai reikia nustatyti ar šie geometriniai objektai susikerta? Tokios problemos sprendimai yra svarbūs animacijoje, kuriant žaidimus bei robototechnikoje. Darbo tema būtų tokia: parašyti konkretų algoritmą kreivių ar paviršių susikirtimui (kolizijai) nustatyti ir jį praktiškai vizualizuoti kokioje nors judančių geometrinių objektų terpėje. Panašūs algoritmai yra nagrinėjami mano skaitome kurse magistrantams "Simboliniai metodai modeliavime".
"Pusiau reguliarus plokštumos padalinimas", vadovas - doc. S.Zubė
Plokštumą galime padalinti trimis skirtingais būdais į reguliarius daugiakampius naudojant trikampius, kvadratus arba šešiakampius. Tačiau yra įdomus ir nereguliarus plokštumos padalinimai į daugiakampius. Tokius padalinimus galima gauti naudojant pavyzdžiui tokią konstrukciją. Erdvėje išsibrėžkime daug vienodų kubų, kurių viršūnės yra sveikose koordinatėse. Tada kirskime tuos kubus pasvirusia plokštuma. Plokštumoje bus iškirstas įdomus daugiakampis (jį reikia vizualizuoti). Kiekvienas kubas, susikertantis su plokštuma, turi sienas, kurios nesikerta su plokštuma. Tos sienos yra dviejų rūšių vienos bus vienoje plokštumos pusėje, kitos - kitoje. Visos vienos rūšies sienos sudaro begalinį paviršių susidedantį iš kvadratų. Bet kurį iš tų paviršių galima projektuoti (pasirinkę projektavimo kryptį) į plokštumą. Plokštumoje gausime daug keturkampių, kurie ir sudarys ne reguliarų plokštumos padalinimą (jeigu plokštuma pasvirusi, kubu atžvilgiu, neracionaliu kampu). Taigi studentų darbas būtų vizualizuoti tokias (ir panašiomis daugiamatėmis konstrukcijomis apibendrintas) ne reguliarias plokštumos padalinimo schemas.
"3D objektų rekonstrukcijos pagal fotografijas", vadovas - doc. R.Krasauskas
Praktikoje yra didelis poreikis sukurti 3D modelius pagal jų plokščius vaizdus (dažniausiai fotografijas). Numatomo darbo tikslas - susipažinti su šiuolaikiniais 3D objektų rekonstrukcijos metodais, praktiškai pritaikant juos vizualizacijos projektui VRML/X3D technologijos pagrindu.
"Poliedrinių paviršių optimizavimas", vadovas - doc. R.Krasauskas
3D geometriniai objektai sukurti standartinėmis modeliavimo priemonėmis paprastai turi per daug trikampių. Tokie dideli failai sukelia įvairių jų perdavimo ir vaizdavimo sunkumų. Be to, dažnai reikia turėti to paties objekto skirtingus detalumo lygius. Numatoma susipažinti su 3D informacijos optimizavimo metodais, praktiškai realizuojant žinomus arba patobulintus algoritmus.
"Modeliavimas naudojant specialius 4-to laipsnio paviršius", vadovas - doc. R.Krasauskas
Geometrinis modeliavimas paprastai vyksta su standartiniu paviršių/kūnų rinkiniu (cilindrai, kūgiai, sferos, torai). Pvz., du vienodo skersmens cilindrus galima glodžiai sujungti naudojant toro segmentą. Tokią standartinių algebrinių paviršių klasę galima natūraliai praplėsti iki specialių 4-to laipsnio paviršių, kurie yra žymiai "lankstesni": pvz., tinka glodžiam kūgių jungimui. Numatomas rezultatas - kompaktiškas modeliavimo paketas, skirtas interaktyviam tokių sudėtinių paviršių sukūrimui ir išsaugojimui pasirinktame formate.
"Kolizijos tarp kvadrikių", vadovas - doc. R.Krasauskas
Kolizijų tarp 3D objektų skaičiavimas - tai labai aktualus realaus laiko kompiuterinės grafikos uždavinys. Nėra sunku apskaičiuoti kada kertasi dvi sferos. Kai turime bendresnius antro laipsnio paviršius (kvadrikes), pvz. elipsoidus, šis uždavinys jau nėra trivialus. Darbas būtų skirtas kolizijų tarp kvadrikių skaičiavimo algoritmams, bei jų vizualizacijai.
"NURBS kreivės ir paviršiai internetinėje grafikoje", vadovas - doc. R.Krasauskas
NURBS kreivės ir paviršiai yra labai patogūs glodžių 3D objektų modeliavimui, taip pat ir internetinėje interaktyvioje grafikoje, nes jie koduojami nedideliu skaičiumi kontrolinių taškų. Problemos atsiranda vaizduojant NURBS'us, kai jie yra smulkinami į tiesinius primityvus (tiesės atkarpas, trikampius). Koks turėtų būti smulkinimo žingsnis, kad būtų pasiektas reikiamas balansas tarp kadrų per sekundę skaičiaus ir vaizdavimo kokybės? Darbas skiriamas šios problemos sprendimui parenkant tinkamas duomenų struktūras ir algoritmus.
"Splaininės kreivės ant paviršių (keli variantai)", vadovas - doc. R.Krasauskas
Kreivių modeliavimas plokštumoje turi ilgą istoriją ir išvystytą teoriją. Tuo tarpu praktikoje pasitaiko situacijos, kada yra svarbu, kad kreivė gulėtų ant duoto paviršiaus. Tada reikia pasitelkti specifines priemones. Darbo tikslas - realizuoti interaktyvią kreivių modeliavimo sistemą ant paprasčiausių paviršių: cilindro, kūgio, sferos, toro, Bezier keturkampio paviršiaus pasirinktinai. Galima naudoti įvairias kompiuterinės grafikos priemones (VRML/X3D, OpenGL).
"Gardelinių daugiakampių unimoduliarinė klasifikacija", vadovas - doc. R.Krasauskas
Gardelinis daugiakampis - tai iškilas daugiakampis plokštumoje, kurio viršūnės turi sveikaskaitines koordinates, t.y priklauso gardelei. Pasirodo, kad geometriniame modeliavime svarbių torinių paviršių klasifikacija susiveda į gardelinių daugiakampių klasifikaciją atžvilgiu tokių afininių plokštumos transformacijų, kurios išlaiko plotus ir gardelę (jos vadinamos unimoduliarinėmis). Turime labai aiškų kombinatorinį uždavinį: surašyti visas gardelinių daukiakampių (kurių plotas neviršyja duotos konstantos) klases į lentelę. Čia natūralu naudoti simbolinio skaičiavimo priemones, pvz. MAPLE paketą, bet galimi ir kiti variantai.
"Trigonometrinės paviršių parametrizacijos (Aprašymas bus)", vadovas - doc. R.Krasauskas
"Realaus laiko grafikos efektai", vadovas - doc. R.Krasauskas ir doktorantas T.Sakalauskas
- Žolės atvaizdavimas realiame laike. Realiame laike atvaizduojant žoles plotus, paprastai naudojamos tekstūros tiesiogiai nupieštos ant landšafto arba "billboard" tipo paveikslėliai kurie visada atsisukę į kamerą. Tai labai sumažina realizma. Darbo tikslas - išnagrinėti alternatyvius metodus, bei realizuoti egzistuojantį ar patobulintą algoritmą.
- Medžių generavimas. Dažna kompiuterinių žaidimų problema yra ta, kad naudojamas ribotas modelių skaičius medžių atvaizdavimui. Šio darbo metu reikėtų išnagrinėti fraktalinius medžių generavimo algoritmus, bei įgyventi parametrizuotą algoritmą įvairios struktūros medžių generavimui ir atvaizdavimui. Vienas is parametrų - detalumo lygis, nusakantis sugeneruoto modelio sudėtingumą.
- Miško atvaizdavimas. Darbo tikslas - progama leidžianti pasivaikščiojimą virtualiame miške. Tam reikia išnagrineti LOD (Levels Of Details) algoritmus, bei juos pritaikyti ar optimizuoti medžių vaizdavimui. Pagrindinis sunkumas - didelis medžiu skaičius, atskirus medžius vaizduojant net paprasčiausiais modeliais gaunamas mažas kadrų per sekundę skaičius, todėl skirtingo detalumo lygio algoritmai privalo veikti medžių grupėms.
- Landšafto generavimas. Darbo metu reikėtų apžvelgti šiuo metu naudojamus landšafto sintezės algoritmus, palyginti jų gaunamus rezultatus. Įgyvendintas algoritmas turėtų sukurti ne tik geometrinį landšafto modelį, bet ir tekstūras atitinkančias reljefą.
- Erozijos modeliavimas. Dauguma fraktalinių algoritmų sugeneruoti landšaftai, neatrodo labai realūs - trūksta kalnams būdingų formų. Panašumą galima padidinti modeliuojant erozijos efektus. Darbo tikslas - sukurti programa, kuri generuoja landšaftą kokio nors egzistuojančio algorimto pagrindu ir simuliuoja to landšafto eroziją.
- Dalelių sistemos (Particle Systems). Dalelių sistemas, dažnai naudojamas kino efektams sukurti, galima įgyvendinti realiame laike. Paprastai tokios realizacijos būna gana paprastos ir gamtinius reiškinius kaip ugnis ar sprogimas atvaizduoja labai nenatūraliai. Vienas is būdų pagerinti dalelių sistemos dinamiką - įvesti papildomas daleles kurios įtakoja aplinkinių dalelių parametrus. Pavyzdžiui dalelė "sukūrys", verčia aplinkines daleles suktis apie jos aši. Pats sukūrys juda pagal visus dalelių sistemos dėsnius, įskaitant kitų sukūrių poveikį. Darbo metu reikėtų realizuoti dalelių sistemą su idomiomis dinaminėmis dalelėmis, kurios pagalba būtų modeliuojami gamtiniai reiškiniai (ugnis, dūmai, krioklys ar pan.)
"Klasikiniai paviršių padalijimo algoritmai", vadovai - doc. R.Krasauskas ir doktorantas S.Narkevičius
Padalijimo algoritmai yra bene pats paprasčiausiai būdas piešti kreives ir paviršius. Pakanka mokėti dalinti tiesės atkarpą pusiau. Šį elementarų veiksmą atlikus daug kartų, be abejo, kompiuterio pagalba, iš "labai tiesių" atkarpėlių gauname "labai šiauniai kreivus" paviršius. Pradedame nuo grubaus keturkampio ar trikampio tinklelio, kuris apytikriai nusako trimatį objektą, pvz. keliasdešimties keturkampių tinklas gali nusakyti pradžioje labai kampuotą pomidorą. Vėliau tinklelis yra vieną kartą pasmulkinamas (padalinamas) atliekant daug vienodų veiksmų atskiroms briaunoms. Gautąjį tinklelį vėl galime pasmulkinti ir gauti dar tikslesnį pomidoro vaizdą. Riboje mes gautume tikslų pomidorą. Praktikoje apsiribojama 4-iais - 6-iais padalijimo žingsniais. Tuomet pomidoras susideda iš kelių šimtų tūkstančių keturkampių ar trikampių ir atrodo idealiai glodus. Akademinė visuomenė tokius paprastus paviršius nuo pat jų atsiradimo 1978 metais vadino "žaisliniais", nepritaikomais trimačio vizualizavimo ar projektavimo sistemose. Situacija gerokai pasikeitė po 1997 metais pasirodžiusio Pixar kino studijos trumpametražinio kompiuterinio animacinio filmuko "Džerio žaidimas" (www.pixar.com/shorts/gg). Jame visi trimačiai objektai buvo aprašyti naudojant padalijimo paviršius. Šis filmukas buvo apdovanotas Oskaru. Šiame darbe susipažinsime su klasikinėmis padalijimo schemomis. Suprogramuosime keletą jų ir palyginsime gautų paviršių vizualinę kokybę. Antrasis tikslas yra pateikti daug padalijimo paviršių iliustracijų, todėl darbo aprašyme ne mažiau kaip pusę ploto turėtų užimti kompiuterio sugeneruoti paveikslėliai. Gautųjų paviršių vaizdavimui ir iliustracijų kūrimui puikiausiai tinka standartinės VRML pasaulių rodymo priemonės ar kitos laisvai prieinamos programos.
"Box-splainų vaizdavimas padalijimo pagalba", vadovai - doc. R.Krasauskas ir doktorantas S.Narkevičius
Pastaba: trumpa įžangėlė į padalijimo paviršius pateikta prie temos "Klasikiniai paviršių padalijimo algoritmai". Box-splainai - puikus matematinis įrankis kreivėms ir paviršiams konstruoti. Matematikai juos mėgsta dėl mielų savybių, kaip glodumas. Trimatės grafikos dizaineriai juos mėgsta dėl malonaus akiai vaizdo. Matematinė šių paviršių prasmė yra gana keblus dalykas. Laimei jų vaizdavimas padalijimo algoritmų pagalba yra visa eile paprastesnis. Šiame darbe susipažinsime su Box-splainais kreivėms ir paviršiams. Keletą jų suprogramuosime ir pavaizduosime. Darbo tikslas - pateikti apibendrintą algoritmą tokių paviršių konstravimui. Pagrindinis akcentas - kreivių ir paviršių vaizdai, todėl darbo aprašyme laukiama daug iliustracijų.
"Padalijimo paviršių glodumo analizė", vadovai - doc. R.Krasauskas ir doktorantas S.Narkevičius
Pastaba: trumpa įžangėlė į padalijimo paviršius pateikta prie temos "Klasikiniai paviršių padalijimo algoritmai". Padalijimo paviršiai nėra tokie "žaisliniai", kaip buvo manyta pačioje jų atsiradimo pradžioje 1978 metais. Žaisliniais jie buvo laikomi dėl sunkiai nusakomų matematinių savybių aplink taip vadinamus "ypatinguosius" taškus. Viena nuostabiausių padalijimo paviršių savybių - galimybė apsirašyti sudėtingos topologijos figūras naudojant elementarius padalijimo veiksmus. "Sudėtingomis" laikomos tos, kurių negalima nusakyti reguliariais kvadratiniais ar trikampiais tinkleliais. Pavyzdžių toli ieškoti nereikia: dauguma gyvenime sutinkamų figūrų, kaip žmonių galvos, automobiliai, buitiniai prietaisai gali būti vadinamos sudėtingomis matematine prasme. Jose tenka tarpusavyje jungti reguliarius tinklelius į sudėtingesnius darinius. Reguliarių tinklelių atveju glodumui tirti naudojami klasikiniai metodai, tačiau jų jungimo (sudūrimo) vietose patogiau taikyti specializuotus analizės metodus. Šiame darbe susipažinsime su keletu padalijimo paviršių bei jų glodumo analize. Analizės metodai bus panaudoti keletai padalijimo schemų analizuoti. Svarbi darbo dalis - glodžių ir neglodžių paviršių vizualizavimas.
"Padalijimo paviršių konstravimas kaukių pagalga", vadovai - doc. R.Krasauskas ir doktorantas S.Narkevičius
Pastaba: trumpa įžangėlė į padalijimo paviršius pateikta prie temos "Klasikiniai paviršių padalijimo algoritmai". Padalijimo paviršius galima konstruoti naudojant vadinamuosius šablonus (stencil) arba kaukes (mask). Abu būdai duoda identiškus rezultatus. Šiuo metu yra labiau įprasta naudoti šablonus. Kita vertus, mąstymas kaukių sąvokomis padeda lengviau apibendrinti daugelį paviršių savybių. Šiame darbe susipažinsime su keletu padalijimo paviršių. Palyginsime jų konstravimą naudojant šablonus ir kaukes. Kaukių sąvokos pagalba iliustruosime pasirinktas paviršiaus savybes.
"Nestacionarūs padalijimo paviršiai", vadovai - doc. S.Zubė ir doktorantas S.Narkevičius
Pastaba: trumpa įžangėlė į padalijimo paviršius pateikta prie temos "Klasikiniai paviršių padalijimo algoritmai". Stacionarūs padalijimo paviršiai turi didelę vaizdavimo išraiškos galią. Todėl iš pirmo žvilgsnio yra labai keista, kad jiems neįkandamos tokios elementarios geometrinės figūros, kaip sfera. Čia į pagalbą ateina nestacionarios padalijimo schemos, t.y. tokios, kuomet padalijimo algoritmas kinta su kiekvienu tinklelio pasmulkinimo žingsniu. Darbo tikslas susipažinti su stacionariais ir nestacionariais padalijimo paviršiais. Reikės suprogramuoti keletą padalijimo schemų ir pateikti sukimo paviršių pavyzdžių: taurės, bokalai, ąsočiai ir pan..
"Ribinio padalijimo paviršiaus vaizdavimas", vadovai - doc. S.Zubė ir doktorantas S.Narkevičius
Pastaba: trumpa įžangėlė į padalijimo paviršius pateikta prie temos "Klasikiniai paviršių padalijimo algoritmai". Naudojant padalijimo algoritmus grubūs bei kampuoti pradiniai karkasai su kiekvienu padalijimo žingsniu spėriai virsta į glodžius paviršius. Toks konvergavimas turi atitinkamą ribinį paviršių. Yra įprasta apsiriboti 4-7 žingsniais, kuomet sugeneruojama daugybė trikampėlių, esančių labai arti ribinio paviršiaus. "Labai arti", tačiau ne ant ribinio paviršiaus. Šiame darbe susipažinsime su keletu padalijimo paviršių. Tikslas - suskaičiuoti bet kuriam tinkleliui jį atitinkančius ribinio paviršiaus taškus. Pavaizduoti "artėjantį prie ribos" ir "riboje esantį" paviršius.
"Padalijimo paviršių dengimas tekstūromis", vadovai - doc. S.Zubė ir doktorantas S.Narkevičius
Pastaba: trumpa įžangėlė į padalijimo paviršius pateikta prie temos "Klasikiniai paviršių padalijimo algoritmai". Praktinis paviršių panaudojimas yra sunkiai įsivaizduojamas be jų dengimo tekstūromis. Jau seniai žinoma, kad paprasčiau pavaizduoti, kad ir grubiai trikampiuotą kalnų landšaftą, uždengiant jį atitinkamomis grunto ir uolų nuotraukomis, negu bandyti modeliuoti kiekvieną akmenėlį atskirai. Šio darbo tikslas - susipažinti su padalijimo paviršiais ir sinchronizuoti taškų koordinačių padalijimo veiksmus su piešinio uždėjimu ant paviršiaus.
"Padalijimo paviršių kraštai", vadovai - doc. K.Karčiauskas ir doktorantas S.Narkevičius
Pastaba: trumpa įžangėlė į padalijimo paviršius pateikta prie temos "Klasikiniai paviršių padalijimo algoritmai". Dauguma padalijimo algoritmų akcentuoja paviršiaus formą jo viduje, o krašto vaizdą ir matematines savybes palieka vartotojo nuožiūrai. Darbo tikslas - susipažinti su padalijimo paviršiais. Panagrinėti galimas paviršiaus krašto sąlygas pagal įvairius kriterijus: vieni paviršiaus kraštai atrodo gražiau, kiti pasižymi norimomis matematinėmis savybėmis ir pan..
"Padalijimo paviršių artefaktai", vadovai - doc. S.Zubė ir doktorantas S.Narkevičius
Pastaba: trumpa įžangėlė į padalijimo paviršius pateikta prie temos "Klasikiniai paviršių padalijimo algoritmai". Pradėjus plačiau naudoti padalijimo paviršius, kartu buvo daugiau sužinota apie jų praktinius taikymo aspektus. Taip pat buvo susidurta su labai nemaloniomis staigmenomis: artefaktais. Gražus ir "natūraliai atrodantis" pradinis karkasas po keletos padalijimo žingsnių davė nepageidaujamus paviršiaus iškilimus arba labai netolygaus dydžio ląsteles tinklelyje. Tokie artefaktai yra labai nepageidaujami kompiuterinėje animacijoje ir visiškai nepriimtini kompiuteriniame projektavime. Šio darbo tikslas yra susipažinti su padalijimo paviršiais ir jų artefaktų tipais. Pateikti artefaktų iliustracijų ir rekomendacijų, kaip jų būtų galima išvengti.
"Padalijimo paviršiai spindulių trasavime", vadovai - doc. S.Zubė ir doktorantas S.Narkevičius
Pastaba: trumpa įžangėlė į padalijimo paviršius pateikta prie temos "Klasikiniai paviršių padalijimo algoritmai". Spindulių trasavimas (ray tracing) yra vienas tikroviškiausių geomtrinių objektų vaizdavimo būdų. Jo pagalba mes nesunkiai gauname kūnų šešėlius, veidrodinius atspindžius ir stiklinių objektų (pvz. lęšių) iškreiptus vaizdus. Spindulių trasavimas savo prigimtimi labiau tinka paviršiams, turintiems matematinę išriašką f(x, y, z)=0. Padalijimo paviršiai, bendru atveju, neturi tokio matematinio pavidalo. Šio darbo tikslas yra susipažinti su padalijimo paviršiais. Taip pat pateikti keletui iš jų spindulių trasavimui reikalingus algoritmus. Tokių būdų mes galėsime pavaizduoti veidrodinį pomidorą šalia stiklinio.
"Padalijimo paviršių kolizijos", vadovai - doc. S.Zubė ir doktorantas S.Narkevičius
Pastaba: trumpa įžangėlė į padalijimo paviršius pateikta prie temos "Klasikiniai paviršių padalijimo algoritmai". Kompiuterinėje animacijoje, kaip ir fizikinių reiškinių modeliavime, dažnai tenka spręsti paviršių susidūrimo (kolizijos) uždavinį. Pvz. iš viršaus ant pasvirusio stalo krentantis obuolys pradžioje atsitrenkia į pasvirusį stalą, o vėliau nurieda jo paviršiumi. Tokį eksperimentą nesunku atlikti namie. Kompiuteryje šiam procesui aprašyti, be kita ko, tenka apskaičiuoti momentą, kada du kūnai susiduria. Šio darbo tikslas yra susipažinti su padalijimo paviršiais. Taip pat pateikti keletui iš jų kolizijos aptikimo algoritmus.
"Padalijimo paviršių generavimas pagal simbolį", vadovai - doc. S.Zubė ir doktorantas S.Narkevičius
Pastaba: trumpa įžangėlė į padalijimo paviršius pateikta prie temos "Klasikiniai paviršių padalijimo algoritmai". Tai gana ambicingas ir nemažai programavimo reikalaujantis uždavinys, skirtas studentų grupei. Yra daug būdų, kaip iš pradinio grubaus karkaso gauti glodų padalijimo paviršių. Kiekvieną iš šių būdų (padalijimo schemų) galima nusakyti simboliu. Šiuo atveju simbolis, tai skaičių ir raidžių seka, lakoniškai ir vienareikšmiškai nusakanti padalijimo schemą, t.y. kaip iš pradinio tinklelio gautį sekantį, smulkesnį. Šio darbo tikslas yra susipažinti su padalijimo paviršiais ir jų generavimą nusakančiais simboliais. Reikės sukurti programą, kuri duotą pradinį karkasą padalintų pagal pasirinktą simbolį (padalijimo schemą). Tai būtų neįkainuojamas įrankis tyrinėjant stacionarias padalijimo schemas, nes beveik visos jos gali būti nusakytos atitinkamais simboliais. Šiuo metu rinkoje galima gauti atskiras programas, realizuojančias tik tam tikras schemas. Jei norite pasibandyti savo sugalvotąją, jums tenka rašyti naują programą.
"Padalijimo paviršių gardelės", vadovai - doc. S.Zubė ir doktorantas S.Narkevičius
Pastaba: trumpa įžangėlė į padalijimo paviršius pateikta prie temos "Klasikiniai paviršių padalijimo algoritmai". Padalijimo paviršiai pradedami generuoti nuo pradinės gardelės, kuri dažniausiai yra sudaryta iš keturkampių ar trikampių. Yra ir kitų topologijų gardelių: šešiakampės, mišrios keturkampės-aštuonkampės. Gardelės pasirinkimas dažnai lemia kitokį ribinio paviršiaus vaizdą. Šio darbo tikslas yra susipažinti su padalijimo paviršiais ir jiems generuoti naudojamomis gardelėmis. Reikės pavaizduoti tuos pačius paviršius, gautus naudojant skirtingas gardeles. Pagrindinis palyginimo kriterijus: estetinis vaizdas (vieni atrodo "natūraliau" nei kiti) ir nepageidaujamų sąvybių (artefaktų) išvengimas.
"Paviršiams lygiagretūs paviršiai (ofsetai)", vadovas doc. K. Navickis
Duotajam paviršiui galima priskirti naują paviršių, vadinamą jam lygiagrečiu paviršiumi arba ofsetu. Kursinio darbo tema būtų tokių paviršių diferencialinės geometrijos nagrinėjimas MAPLE paketo pagalba.
"Palūkanų normų struktūros laike modeliavimas", vadovas doc. K. Navickis
Pastaraisiais dešimtmečiais buvo pasiūlyti įvairūs palūkanų normų laiko struktūros teoriniai modeliai. Kursiniame darbe būtų nagrinėjami populiariausi iš šiuolaikinių modelių.
"Procentiniai finansiniai instrumentai", vadovas doc. K. Navickis
Šiuolaikinėse finansų rinkose egzistuoja labai daug įvairiausių finansinių instrumentų. Kursiniame darbe būtų nagrinėjami tokių instrumentų įverčiai.
"Finansinė rizika ir jos valdymas", vadovas doc. K. Navickis
Žmonių, firmų ir visuomeninių institutų aktyvumas, nukreiptas išsaugoti ir pagerinti savo gerbūvį, numato rizikos galimybių nagrinėjimą. Kursiniame darbe būtų nagrinėjamas rizikos valdymas finansinėse rinkose.
"Solitonai ir Beklundo transformacijos", vadovas doc. K. Navickis
Solitonų teorija padarė ženklią įtaką tiek fizikai, tiek matematikai. Kursiniame (bakalauro ar magistro) darbe būtų nagrinėjamos kelios pagrindinės evoliucinės diferencialinės lygtys, jų sprendinių savybės MAPLE paketo pagalba.
"Užsienio valiutų rinka", vadovas doc. K. Navickis
Valiutos kursas leidžia vartotojams ir gamintojams vienoje šalyje pakeisti kita valiuta nustatytas prekių, paslaugų, išteklių ir turto kainas į savo pačių valiutą, kad galėtų tiksliai palyginti vertes. Kursiniame darbe būtų nagrinėjama užsienio valiutų rinka, kursų svyravimai, palūkanų normos ir infliacija.
"Geodezinės kreivės", vadovas doc. K. Navickis
Vizualizuoti paviršiaus geodezines kreives geometrams visada buvo sunku.Tai susiję su tuo,kad geodezinių kreivių lygtys bendruoju atveju gali būti išspręstos tik skaitiniais metodais.Kursiniame darbe būtų nagrinėjama paviršių geodezinių kreivių vizualizacija MAPLE paketo pagalba.
"Pseudosferiniai paviršiai", vadovas doc. K. Navickis
Pseudosferinius paviršius pradėjo nagrinėti F.Mindingas 1838 m. L.Bianki 1879 m. pateikė tokių paviršių geometrinę konstrukciją.Ją 1883 m. modifikavo A.Beklundas. Kursiniame darbe būtų nagrinėjama pseudosferinių paviršių geometrija MAPLE paketo pagalba.
"Fraktalinės kreivės", vadovas doc. K. Navickis
Fraktalinė geometrija susijusi su nereguliarių aibių nagrinėjimu.Fraktalai turi taikymus kompiuteriniame dizaine,informacijos suspaudimo algoritmuose ir kt.Šiuo metu fraktaliniai objektai labai populiarūs. Kursiniame darbe būtų nagrinėjamos fraktalinės kreivės (Sierpinskio,Peano, Kocho,Mengerio ,drakonai) MAPLE paketo pagalba.
"Paviršių rekonstravimas iš pirmosios kvadratinės formos koeficientų", vadovas doc. K. Navickis
Paviršių padėties erdvėje tikslumu apibrėžia jo pirmoji kvadratinė forma (teigiamai apibrėžta) ir antroji kvadratinė forma.Šių formų koeficientai tenkina Gauso-Veingarteno lygtis. Kursiniame (bakalauro ar magistro) darbe būtų nagrinėjamas paviršiaus rekonstravimas,kai žinoma jo pirmoji kvadratinė forma, MAPLE paketo pagalba.
"Matematinės ekonomikos modeliai ir jų vizualizacija", vadovas - prof. F. Ivanauskas
Tokie ekonomikos atributai, kaip akcijos, draudimai, kilnojamas ir nekilnojamas turtas, pirkimai ir pardavimai yra aktualūs ne tik asmeniniame žmogaus gyvenime, bet ir firmų bei organizacijų veikloje. Vertinant ir tiriant tokius ekonominius reiškinius ir procesus, daugeliu atvejų reikia taikyti matematinius modelius. Darbe nagrinėjami ir tiriami matematinės ekonomikos modeliai, daugiausia kurie aprašomi diferencinėmis ar panašiomis lygtimis. Daug dėmesio bus skiriama tinkamiems vizualizacijos metodams.
"Medienos džiovinimo matematinis modeliavimas", vadovai - prof. F. Ivanauskas ir dr. R. Baronas
Medienos džiūvimo procesas yra sudėtingas reiškinys, svarbus daugelyje pramonės šakų. Jis dar nėra detaliai ir pilnai žinomas. Todėl pasaulyje atliekama daug šio proceso tyrimų. Numatoma medienos džiūvimo procesą modeliuoti šilumos laidumo lygtimis, ar kitokiais panašiais matematiniais modeliais. Šitokio modeliavimo metodika gali būti taikoma ir kituose reiškiniuose: elektrochemijoje, biochemijoje ir pan. uždavinius. Todėl atliekant šį darbą, bus ne tik gaunami rezultatai, bet ir įgyta vertinga modeliavimo patirtis.
"Paukščių migracijos ir perskridimų tyrimas duomenų analizės priemonėmis", vadovai - prof. F. Ivanauskas ir doc. A. Juozapavičius
Lietuvos ornitologų draugija yra sukaupusi daug duomenų apie paukščių parskridimus į Lietuvą ir jų išskridimus, apie paukščių migraciją į įvairias šalis ir kontinentus. Tik maža tokių duomenų dalis yra ištirta ir išanalizuota, nors migracijos svarba yra didelė. Paukščių judėjimo žinojimas leidžia projektuoti saugesnius lėktuvų judėjimo maršrutus, tiksliau prognozuoti klimato pasikeitimus, vertinti kitus svarbius žmogaus veiklai faktorius (žuvivaisą, derlius, ir pan.), taipogi tirti klimato atšilimo įtakos Lietuvoje pobūdį. Daug duomenų yra ir Internete. Pasitelkiant šiuos duomenis ir tinkamus programinės įrangos paketus (pvz. duomenų analizės (data mining)), numatoma ištirti įvairiarūšes duomenų sąsajas ir jas vizualizuoti, o svarbiausia, padaryti įdomias ir turiningas išvadas.
"Procesų lazeriuose modeliavimas ir vaizdavimas", vadovas - prof. F. Ivanauskas
Lazeriai vaidina labai didelę rolę tiek moksle, tiek gamyboje. Studentai kviečiami dalyvauti su lazeriais susijusių uždavinių sprendime ir skaičiavimuose, duomenų ir rezultatų analizėje, taip pat kurti tinkamas šiai sričiai kompiuterinės grafikos priemones.
"Elektrochemijos uždavinių modeliavimas", vadovas - prof. F. Ivanauskas
Mikroelektrodai plačiai taikomi šiuolaikinėse technologijose ir medicinoje. Studentų darbas ir įdėjos būtų vertingi atliekant skaičiavimus, vizualizuojant duomenis ir rezultatus, interpretuojant juos.
"Biochemijos uždavinių sprendimas", vadovas - prof. F. Ivanauskas
Biocheminiai mikroreaktoriai vaidina svarbų vaidmenį įvairiuose taikymuose, ypač farmakologijoje ir chemijos pramonėje. Juos modeliuojant Kompiuterijos katedra jau keli metai dirba bendrai su Biochemijos institutu, yra sukaupta solidi skaičiavimų ir rezultatų analizės patirtis. Studentams siūloma įsitraukti į šiuos tyrimus, atitinkamus skaičiavimus, rezultatų vizualizaciją, dalyvauti Europos Sąjungos projekte.
"Trimačių geometrinių objektų ir figūrų vizualizacija Internete", vadovas - doc. A.Juozapavičius
Geometrinės figūros, ypač trimatės (briaunainiai, sferos ir pan.), ir kompleksai, sudaryti iš jų, yra labai populiarūs vizualizuojant objektus daugelyje taikomųjų sričių (kompiuterinėje grafikoje, chemijoje, biologijoje, vaistų konstravime, fizikoje, architektūroje, statybinėse konstrukcijose ir pan.). Darbo tikslas yra, panaudojant tinkamas Interneto technologijas: dinaminius HTML puslapius, JAVA, sukurti arba įsisavinti programines priemones, kurių pagalba būtų galima dinamiškai ir interaktyviai vaizduoti geometrines figūras Web puslapiuose. Vykdant šį darbą, pagrindinė programavimo priemonė galėtų būti JAVA programavimo kalba arba Macromedia Flash paketas, kuriuos galima išmokti darbo metu.
"Duomenų bazių indeksų vizualizavimas", vadovai - doc. A.Juozapavičius ir doktorantas K.Mickus
Kuriant ar projektuojant duomenų bazes, projektuojant ir diegiant greitas paieškos/keitimo operacijas, yra pasiūlyta daugiamačių duomenų išrinkimo metodų, ar tiesiog daugiamačių indeksinių duomenų struktūrų. Darbo tikslas yra sukurti duomenų bazių indeksų, ypač hierarchinių duomenų struktūrų vizualizavimo priemones, tinkamas jų efektyvumui tirti. Efektyvumas gali būti matuojamas įvairiais parametrais, pvz, I/O operacijų skaičiumi, procesoriaus apkrovimu, sudėtingumo įverčiais ir pan. Vizualizacija gali būti pritaikyta kokio nors "realaus scenarijaus" simuliacijai (pvz, automagistralių ar avialinijų modeliavimas).
"Aplikacijos mobiliose komunikacijose", vadovas - doc. A.Juozapavičius
Dabartiniu metu, paplitus mobiliems telefonams ir mobiliems kompiuteriams (tokiems kaip PDA), labai trūksta taikomųjų uždavinių (aplikacijų). Ši tema ir skirta įvairioms galimų aplikacijų mobiliuose tinkluose idėjoms iškelti, jas išbandyti, pabandyti realizuoti. Studentai ne tik turės sugalvoti galimą aplikaciją, ne tik atlikti jos pilotinę realizaciją, bet ir įvertinti jos galimą rinkos vertę (kad laiku apsaugoti savo intelektualinės nuosavybės teises).
"Mobilių objektų indeksavimas duomenų bazėse", vadovai - doc. A.Juozapavičius ir doktorantas A.Čivilis
Mobilių objektų (mobilių telefonų, mobilių kompiuterių, kt.) populiarumas ir jų gausa kelia visiškai naujus uždavinius mobilius objektus registruojančių kompiuterių architektūrai, tame tarpe duomenų bazėms. Ši tematika dabar labai populiari pasaulyje, ir labai svarbi firmoms, organizuojančioms mobilių duomenų bazes. Darbo tikslas yra susisteminti jau pasiūlytus metodus mobiliai informacijai indeksuoti, ir juos išanalizuoti. Kadangi mobilių duomenų aibės yra labai didelės, reikalingi specialūs metodai ir algoritmai šioms aibėms ir jų indeksams vizualizuoti. Todėl darbe reikia taipogi ištirti įvairius vizualizacijos metodus, juos pritaikyti mobilių duomenų indeksų analizei.
"Informacijos klasifikavimo priemonės", vadovas - doc. A.Juozapavičius
XML kalba vis labiau naudojama apibrėžiant duomenų turinį, konstruojant duomenų bazes. Vis labiau plinta duomenų bazės, saugančios duomenis specifikuotus XML formate, o jų vizualizacijai naudojančios tam tikras duomenų dėstymo schemas. Darbo tikslas yra susipažinti su pasiūlytais metodais specifikuoti duomenis, išbandyti juos konkrečioje tematikoje ir konkrečioje aplinkoje, įvertinti funkcionalumą, sukurti ir įvertinti tinkamas paieškos strategijas, įdiegti atitinkamą vizualizaciją.
"Kompiuterinės regos algoritmai ir sistemos", vadovas - doc. A.Juozapavičius
Kompiuterinė rega kasdien atranda vis naujus taikymus, nuo elementariausių sekimo video kamerų iki robotų ar jų sistemų, sugebančių "protingai" elgtis gana sudėtingose situacijose. Beveik bet kurios iš tokių kompiuterinės regos sistemų pagrindą sudaro vaizdo akvizicija, bazinių elementų (bazinės geometrijos) atpažinimas, objektų modeliavimas, šie procesai turi tenkinti laikinius apribojimus. Darbo tikslas - analizuoti pagrindinius kompiuterinės regos algoritmus, juos realizuoti pasirinktam taikomajam uždaviniui. Pavyzdžiui, gali būti suprojektuota ir įdiegta automobilių sekimo (ir įsiminimo) sistema, kuri sugebėtų sekti net ir naktį važiuojančius (ir be šviesų) automobilius, atpažinti jų tipus.
"Medicininių vaizdų segmentavimas, sluoksniavimas, atpažinimas", vadovai - doc. A.Juozapavičius ir doktorantas J.Skučas
Darbo tikslas yra susipažinti su objektų, jų kontūrų išskyrimo vaizduose metodais - paprastai toks procesas vadinamas vaizdų segmentavimu. Dabartiniai segmentavimo metodai yra gana detalizuoti pilkiems vaizdams, tačiau beveik nėra procedūrų, segmentuojančių spalvotus vaizdus. Reikia šiuos metodus analizuoti, įvertinti, modifikuoti. Tokie metodai yra labai svarbūs tolimesniam vaizdų apdorojimui: objektų analizei, vaizdų duomenų bazių formavimui, vaizdų paieškos indeksų kūrimui, vaizdų kompresijai, ir pan. Darbo rezultatu turėtų būti eksperimentinė kompiuterinė sistema, segmentuojanti ir sluoksniuojanti įvairiarūšius vaizdus, pvz. debesis iš palydovų gaunamose nuotraukose, arba Lietuvos kraštovaizdį (ar dar ką nors).
"Archeologinių objektų interaktyvus vaizdavimas, rekonstrukcija ir modeliavimas", vadovas - doc. A.Juozapavičius
Darbo tikslas yra sukurti interaktyvią kompiuterinę sistemą, kuri tarnautų kaip įrankis archeologiniuose tyrinėjimuose. Ši sistema turėtų pagelbėti archeologams vaizduoti trimatėje erdvėje jų randamų iškasenų liekanas, juos pristatyti įvairiarūšėje aplinkoje, aprašyti, kaupti reikiamą statistiką arba kitus duomenis reikalingus modeliavimui. Ši sistema būtų kuriama bendraujant su VU Istorijos fakultetu (archeologijos katedra).
"Geologinių duomenų analizė (data mining) ir vizualizacija", vadovai doc. A.Juozapavičius ir doktorantas Valdas Rapsevičius
Dabartiniu metu yra surinkta daug geologinio pobūdžio duomenų (apie Lietuvos geologinių sluoksnių sandarą), kurių analizė duotų daug konceptualios informacijos. Darbe numatoma atlikti geologinių duomenų analizę, iškelti ir patikrinti įvairias hipotezes, sudaryti duomenų vizualizacijos scenarijus.
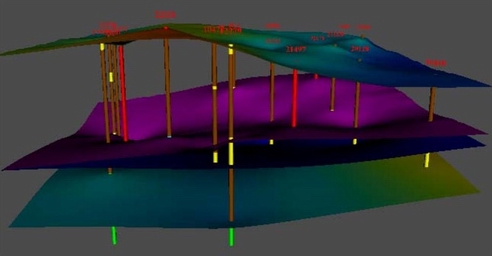
Žemės gelmių geologinės struktūros 3D vizualizacija, vadovai doc. A.Juozapavičius ir doktorantas Valdas Rapsevičius
Žemės gelmės pasižymi sudėtinga vidine sandara, o duomenys apie jas yra santykinai labai skurdūs gręžinių pjūviai. Gręžinys apibrėžiamas geografinėmis koordinatėmis (X, Y), altitude ir kirstų sluoksnių pjūviu. Altitudės reikšmės formuoja vietovės Žemės paviršių, o sluoksnių gylis žemiau slūgsančius paviršius. Santykiai tarp minėtų paviršių gali būti labai įvairūs: lygiagretūs, nedarnos (kertasi, vienas nupjauna kitą), facijinis perėjimas (nuoseklus perėjimas iš vieno į kitą), lūžiai ir pan. Darbo metu reikia suklasifikuoti sluoksnių santykius į klases ir bandyti rasti sprendimus jų atvaizdavimui. Darbo metu bus dirbama su tikrais Žemės gelmių registro duomenimis.
"Vizuali trimatė duomenų analizė", vadovas - doc. A.Juozapavičius
Pastaraisiais metais duomenų srautai ir saugomų duomenų kiekis labai išaugo, kompanijos pradeda saugoti net ir menkiausios svarbos informaciją. Dažnai duomenys yra renkami automatiškai: kasos aparatai, bankomatai, WWW-logai generuoja gigabaitus informacijos kiekvieną dieną. Kompanijos tikisi, kad surinktų duomenų analizė padės konkurencinėje kovoje. Duomenų analizės (angl. data mining - DM) tikslas - atrasti sąryšius ir struktūras duomenų aibėje. Vizuali duomenų analizė (angl. visual data mining - VDM) yra tinkamiausia šiam tikslui: ji apjungia skaičiuojamąją kompiuterių galią ir žmogaus vaizdines galimybes. Darbo tikslas yra kurti kompiuterines priemones, kurios naudoja tankio paviršių (ang. Density Surfaces - DS) metodą, jo pagalba sudaro vizualias struktūras, brėzia tam tinkamus paviršius. DS žymiai supaprastina duomenų interpretaciją, net jeigu duomenų aibė yra didelė ir turi triukšmų. Be to, keičiant tankumo lygį yra imanoma nagrinėti vidinę taškų sankaupos struktūrą.
"Struktūrų atskyrimas 3D duomenų aibėje", vadovas - doc. A.Juozapavičius
Darbo tikslas - padalinti duomenų aibę į nesidengiančius poaibius (taškų sankaupas), tada galima pradėti duomenų sankaupų analizę (angl. clustering analysis), pereinant prie vizualizavimo metodų panaudojimo. Pagrindinis tikslas būtų sukurti metodą, kuris sugebėtų vizualiai ar automatiškai atskirti struktūras, esančias viena šalia kitos. Sukurtas metodas turės būti implementuotas C/C++ kalba. Metodo implementacijai gali būti naudojama 3DVDM sistema: http://www.cs.auc.dk/3DVDM/software.html
"Navigacijos scenarijų vizualizacija", vadovas - doc. A.Juozapavičius
Tankio paviršių (DS) metodas, aprašytas aukščiau, gali būti naudojamas paslėptų ir neakivaizdžių sąryšių studijavimui duomenų aibėje. Tokiu būdu analitikui būtų pasiūlomas parodomasis turas (Fly-through Scenario - FTS). Iš esmės, FTS susideda iš kreivės ir krypčių, apibrėžtų ant jos vizualizavimu. Skrisdamas šia kreive "analitikas" aplankytų tankiausius (rečiausius) duomenų aibės regionus. Toks analizės scenarijus garantuotų, kad analitikas aplanko ir ištyrinėja svarbiausias duomenų aibės struktūras. Kreive galėtų būti spiralinė kreivė ant tankio paviršiaus. Darbo tikslas - vizualizuoti parodomuosius turus. Turint paprasčiausią kelią su kryptimis (trimačiu taškų vektoriumi) studentams reikėtų vizualizuoti analitiko skrydį erdvėje. Taip pat būtų įdomu išanalizuoti skrydžių savybes: greičio, pagreičio, krypties keitimo, tolydaus/netolydaus skrydžio poveikį. Sukurtas metodas turės būti implementuotas C/C++ kalba. Metodo implementacijai gali būti naudojama 3DVDM sistema: http://www.cs.auc.dk/3DVDM/software.html
"Dinaminis skaičiavimų vizualizavimas ", vadovai - doc. F.Ivanauskas ir doktorantas A.Kurtinaitis
Programinės įrangos paketai, skirti moksliniams skaičiavimams, tokie kaip MAPLE, MATLAB, MATHEMATICA, specializuoti diferencinių lygčių sprendimo paketai, arba iš UNIX sistemos kilę paprogramių rinkiniai, sugeba ne tik atlikti reikiamus skaičiavimus, bet ir vizualizuoti rezultatus. Deja, dauguma jų leidžia pavaizduoti tik užbaigto skaičiavimo rezultatą. Tačiau dažnai yra labai naudinga matyti tarpinių skaičiavimų rezultatų vaizdą, o taip pat jų kitimo tendencijas. Darbo tikslas - vizualizuoti skaičiavimo procesą "eigoje" arba "animuoti" skaičiavimus. Darbo metu būtų dirbama su C++ klasių biblioteka VTK, kuri šiuo metu labai populiari ir naudojama daugelyje universitetų ir firmų. Konkrečiai, reikėtų sukurti modelį kreivių ir paviršių dinaminiam vizualizavimui ir jį realizuoti.
"Skaitinių tiesinės algebros metodų optimizacija", vadovas - doc. T.Meškauskas
Praktikoje inžineriniuose skaičiavimuose, sprendžiant ekonominius, fizikinius ir kitus modelius didžiąją dalį kompiuterinių skaičiavimų laiko užima paprasčiausių tiesinių algebrinių lygčių sistemų sprendimas arba matricų tikrinių reikšmių ir tikrinių vektorių paieška. Dažniausiai, nors matricos eilė yra didelė (gali siekti 100000), tik nedaugelis matricos elementų yra nelygūs nuliui. Tokia matrica vadinama išretinta. Pasirinkę šią temą išmoksite pasinaudoti bibliotekomis (BLAS, LAPACK, SPARSKIT ir kt.), realizuojančiomis skaitinius metodus tiesinės algebros uždaviniams. Dauguma šių metodų yra iteraciniai, taigi skaičiavimų apimtis tuo didesnė, kuo tiksliau norime rasti sprendinio artinį. Nagrinėsime, kaip kontroliuojant skaičiavimų tikslumą vidinėje iteracijoje galima ženkliai optimizuoti algoritmą. Programavimas Fortrano arba C++ kalbomis.
"Spektrinės signalų analizės taikymai", vadovas - doc. T.Meškauskas
Pasirinkę šią temą analizuosite ne tik skaitmeninius garso signalus, tačiau ir kitus duomenis, kurie gali būti apdoroti kompiuteriu. Pavyzdžiui valiutų ir akcijų kursai, žmogaus širdies veikla, pirminių skaičių išsidėstymas ir kt. Darbo metodas bus paremtas spektrine duomenų analize žemuose dažniuose. Jeigu triukšmas (signalas) užduotas visiškai atsitiktinių, tarpusavyje nesusijusių skaičių seka, jis skamba šiurkščiai, šnypščiančiai. Taip yra todėl, kad signale esanti energija (galia) susieta su vienodais dažnių intervalais, o ne su oktavomis. Būtent, tokiame signale yra tas pats energijos kiekis pvz. intervale nuo 0 iki 500 Hz, kaip ir nuo 500 iki 1000 Hz arba nuo 20000 iki 20500 Hz. Žmogaus ausiai daug priimtinesnis signalas, kuris turi tą patį energijos kiekį kiekvienoje oktavoje, pvz. dažnių intervale nuo 200 iki 400 Hz ir dažnių intervale nuo 2000 iki 4000 Hz. Pasirodo, būtent tokio tipo signalai stebimi įvairiose srityse (ekonomikoje, medicinoje, astronomijoje ir kt.). Reikės parašyti efektyvias kompiuterines programas, skirtas generuoti ir analizuoti įvairias spektrines savybes turinčius signalus. Galimas bendradarbiavimas su studentais, pasirinkusiais doc. A.Basčio siūlomas temas "Elektrokardiogramų kompiuterinė analizė" ir "Biosignalų kompiuterinė analizė".
"Chaotinių sistemų modeliavimas kompiuteriu", vadovas - doc. T.Meškauskas
Dažniausiai neįmanoma tiksliai nuspėti tolimos sudėtingų procesų ateities. Pavyzdžiui, prognozuoti orus kelioms dienoms į priekį nelengva, o kelioms savaitėms neįmanoma. Truputį pakeitus sistemos parametrus (netgi kompiuterinių paklaidų ribose) sistema gali evoliucionuoti pagal visiškai kitą scenarijų (tarsi vos vos pajudinta moneta gali nuvirsti ant vienos arba ant kitos briaunos). Tokia sistema vadinama chaotine. Su chaotinėmis sistemomis susiduriama ekonomikoje, meteorologijoje, medicinoje ir kitur. Pasirinkę šią temą išmoksite kompiuteriu spręsti tokio tipo modelius, įvertinti sprendinio chaotiškumo laipsnį. Sužinosite kaip tokiai sistemai darant apgalvotą poveikį galima pasiekti sinchronizaciją.
"Lazerių fizikos laboratorija kompiuteryje", vadovas - doc. T.Meškauskas
Pasirinkę šia temą įsisavinsite metodus, naudojamus modeliuojant netiesinės optikos (lazerių fizikos) reiškinius kompiuteriu. Be kitų taikymų, lazeriniai impulsai naudojami duomenų perdavimui šviesolaidžiais. Reikės sukurti programines priemones, leidžiančias interaktyviai įvesti duomenis, skaitiškai išspręsti matematinį modelį, vizualizuoti gaunamus rezultatus. Galimas bendradarbiavimas su kolegomis, pasirinkusiais prof. F.Ivanausko siūlomą temą "Procesų lazeriuose modeliavimas ir vaizdavimas".