RIMANTAS GRIGUTIS

 

KEITINIAI. SIMETRINĖ GRUPĖ Sn

Tegu V = {v1, v2, …, vn} - baigtinė, visiškai sutvarkyta aibė: v1 < v2 < … < vn ir
p - šios aibės keitinys (w1,w2, …, wn). Tuo pačiu žymeniu p žymėsime ir funkciją
p : V ® V; p (v1) = w1, p (v2) = w2, …, p (vn) = wn.

Žinome, kad keitiniai yra abipus vienareikšmės funkcijos ir jų yra n!.

Pateiksime keitinių reiškimo būdus.

1. Keitinio, kaip funkcijos, apibrėžtos baigtinėje aibėje, reiškimas lentele:

2. Reiškimas grafu. Grafas sudarytas iš viršūnių vi, ir orientuotų briaunų
<vi, p (vi)>, 1 £ i £ n.

Pavyzdys:

V = {1; 2; 3; 4; 5; 6; 7}

 

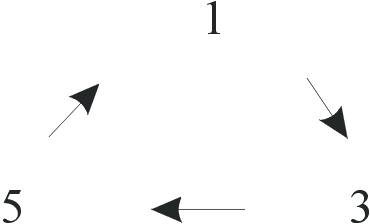
2 « 4, 6, 7

3. Reiðkimas nepriklausomais ciklais.

Tegu vi Ī V . Tada turime aibės V elementų seką

vi, p (vi), p 2(vi) = p (p (vi)), …, p k-1(vi), p k(vi) = vi.

Gauname k ilgio ciklą (vi, p (vi), p 2(vi) = p (p (vi)), …, p k-1(vi)).

Jeigu k = n , tai visi aibės V elementai yra šiame cikle. Kitu atveju, egzistuoja vj Ī (vi, p (vi), p 2(vi) = p (p (vi)), …, p k-1(vi)), kuriam konstruojame savo ciklą:

(vj, p (vj), p 2(vj) = p (p (vj)), …, p l-1(vj)).

Cikluose yra skirtingi elementai.

Jeigu p r(vj) = p s(vi), tai p r+1(vj) = p s+1(vi), …, vj = p l(vj) = p s+(l-r)(vi), tai elementas vj priklausytų pirmajam ciklui, o tai prieštarautų sąlygai.

Taigi, visi aibės V elementai suskyla į nepriklausomus ciklus keitinio p atžvilgiu. Mes jau buvome susidūrę su ekvivalentumo sąryšį atitinkančiu aibės skaidiniu (sveikieji skaičiai kuriuo nors moduliu).

Keitinį p atitinka baigtinės aibės V skaidinys Sp .

vi ŗ vj (mod p ) Ū vj = p s(vi), sĪ N.

Tai ekvivalentumo sŕryđis:

  1. vi ŗ vi (mod p );
  2. vi ŗ vj (mod p ) Ū vj ŗ vi (mod p ),

    vj = p s(vi) ” p k-s(vj) = (vi);

  3. vi ŗ vj (mod p ), vj ŗ vk (mod p ) ” vj ŗ vk (mod p ),

vj = p s(vi), vk = p t(vj) = p t(p s(vi)) = p s+t(vi).

Parodėme, kad bet kurį keitinį galima užrašyti kaip poromis nepriklausomų ciklų “sandaugą”. Šis skaidinys yra vienintelis ciklų išsidėstymo tikslumu.

Paaiškinsime “sandaugos” sąvoką.

Apibrėžimas:

Tegul p , p – keitiniai aibėje V. Keitinių sandauga s = p o p vadinsime keitinį, apibrėžtą lygybe

s (vi) = p(p (vi)), " viĪ V.

Pastebėsime, kad taip apibrėžta sandauga yra funkcijų kompozicija. Ji nėra komutatyvi.

Pavyzdys:

Kai p = , o p = , tai p o p = ¹ = po p .

Tačiau keitinio p kanoniniame skaidinyje esantys nepriklausomi ciklai komutuoja poromis.

Teiginys:

Tegu S(V) - visų keitinių aibė aibėje V . Tada (S(V),  ) - grupė.

Įrodymas.

  1. Operacijos korektiðkumas: jei p , p Ī S(V), tai p o pĪ S(V).
  2. Asociatyvumas: (p o p)o t = p o (po t ),

    ((p o p)o t )(vi) = t ((p o p)(vi)) = t (p(p (vi))) = (po t )(p (vi)) = (p o (po t ))(vi).

  3. Neutralaus elemento egzistavimas: id(vi) = vi, " viĪ V, todėl
    id    o p = p o id = p , p Ī S(V).
  4. Atvirkðtinio elemento egzistavimas: jei p (vi) = wi, tai p -1(wi) = vi.

Įrodyta.

Apibrėžimas:

Ciklas (vI, vj) vadinamas transpozicija.

Teiginys:

Kai |V| ³ 2 ,tai bet kurį keitinį galima užrašyti transpozicijų sandauga.

Įrodymas.

Šį teiginį pakanka įrodyti k ilgio ciklui.

Indukcija pagal k . Kai k = 1, (v) =(u, v) o (u, v),

Kai k = 2; (u, v) =(u, v) ,o

k ³ 3; (v1, v2, …, vk) =(v1, v2) o (v1, v3) o … o (v1, vk). Sandaugoje yra k – 1 transpozicija.

Įrodyta.

Pastebėsime, kad keitinio reiškimas transpozicijų sandauga yra nevienareikšmiškas. Pavyzdžiui,

(v, u) =(v, u) o (v, u) o (v, u).

Pastovus dydis šiame reiškime vis dėl to yra: tai transpozicijų skaičius mod 2.

Apibrėžimas:

Tegu p Ī S(V ). Pora (vi, vj), kai vi < vj , bet p (vi) > p (vj), vadinama keitinio p inversija.

p vadinamas lyginiu keitiniu, jeigu p inversijų skaičius yra lyginis.

p vadinamas nelyginiu keitiniu, jeigu p inversijų skaičius yra nelyginis.

Keitinio p inversijų skaičių žymėsime |p |, o ženklą sgnp = (-1)|p |.

Pastebėsime, kad id yra lyginis keitinys. Jei p - lyginis, tai sgnp = 1, jei p - nelyginis, tai sgnp = -1.

Teiginys:

|p o (a, b)| ŗ |p | + 1 (mod2).

Įrodymas.

p = ,

p o (a, b) = .

Pažymėkime:

pa = |{a1, …, ak| ai > a}|, qa = |{a1, …, ak| ai > b}|,

pb = |{b1, …, bl| bi > a}|, qb = |{b1, …, bl| bi > b}|,

pc = |{c1, …, cm| ci > a}|, qc = |{c1, …, cm| ci > b}|,

Tegu r - keitinio

inversijų skaičius.

Tada, kai a < b, turime

|p | = pa + (l - pb) + (m - pc) + qa + qb + (m - qc) + r,

|p o (a, b)| = pa + pb + (m - pc) + qa + (l - qb) + (m - qc) + 1 + r.

Todėl |p | - |p o (a, b)| = 2(qb –pb) +1 ŗ 1 (mod 2).

Atvejis, kai a > b nagrinėjamas analogiškai.

Įrodyta.

Turime, kad sgn (id) = 1 ir sgn ((a, b)) = -1 .

Transpozicijų skaičius keitinyje p yra pastovus dydis mod 2 . Jeigu turime du keitinio p reiškimus transpozicijų sandauga:

p = s 1 … s k = t 1 … t l,

tai sgnp = sgn(s 1 … s k) = sgn(t 1 … t l) ir sgnp = (-1)k = (-1)l ” (-1)k-1 = 1 ”
k-l ŗ 0 (mod 2) ” k ŗ l(mod 2).

Iðvados:

  1. Keitinys yra lyginis tada ir tik tada, kai jis yra lyginio skaičiaus transpozicijų sandauga.
  2. Keitinys yra nelyginis tada ir tik tada, kai jis yra nelyginio skaičiaus transpozicijų sandauga.
  3. k-ciklas yra lyginis tada ir tik tada, kai k yra nelyginis ir atvirkščiai.
  4. (lyginis) o (lyginis) = (lyginis).

(nelyginis) o (nelyginis) = (lyginis).

(nelyginis) o (lyginis) = (nelyginis).

5. sgn (p o p) =sgn(p )× sgn (p).

Lyginių keitinių aibę žymėsime An.

Teiginys:

An yra grupė.

Įrodymas.

Akivaizdu. Šią grupę vadina alternuojančia grupe.

Įrodyta.

Teiginys:

Lyginių ir nelyginių keitinių yra po lygiai n!/2.

Įrodymas.

Nagrinėjama alternuojanti grupė An. Apibrėžiama aibė

U(a, b) = {p Ī Sn| p = s o (a, b), s Ī An} Ķ Sn - An.

Tegu |An| = m1, | Sn - An| = m2. Tada aibės U(a, b) visi elementai skirtingi:

s 1 o (a, b) = s 2 o (a, b) Ū s 1 o (a, b) o (a, b) = s 2 o (a, b) o (a, b) Ū s 1 = s 2.

Taigi, |U(a,b)| = |An| = m1 £ m2.

Analogiškai, tarkime, turime aibę

W(a,b) = {p Ī Sn| p = p o (a, b), p Ī Sn - An } Ķ An.

Kaip ir aibės U(a,b), taip ir aibės W(a,b) visi elementai skirtingi.

Tada W(a,b) = | Sn - An| = m2 £ m1.

Taigi, m1 = m2 = n!/2.

Įrodyta.

Teorema(A.Cayley):

Tegu (G, × ) yra baigtinė grupė, turinti n elementų. Tada egzistuoja funkcija
f : G ® S(G) =Sn, tenkinanti savybes:

f(g1)=f(g2) Ū g1=g2 (injektyvumas),

f(g× h)=f(g) × f(h) (homomorfizmas).

Įrodymas.

" aĪG konstruojame keitinį La : G ® G , La(g) =g × a . Taigi La Ī Sn.

Turime aibių lygybę

{g1, g2, ..., gn} = {g1× a, g2× a, ..., gn× a} = G.

Turime

1) LaĪ Sn;

2) (La)-1 = La-1

3) La× b(g) = g × (a × b) = (g × a) × b = Lb(La(g)) = (La o Lb)(g), taigi La× b = La o Lb.

Gavome, kad keitiniai Lg1, Lg2, ..., Lgn sudaro grupę H Ģ S(G) = Sn.

Funkcija f : G (r) H Ģ Sn apibrėžta formule f(g) =Lg.

Įrodyta.

Pavyzdys 1

Rombo simetrijų grupės įdėjimas į simetrinę grupę.

Tegu G = {e, a, b, c} - rombo simetrijų grupė. Čia e ir a posūkiai atitinkamai 0° ir 180° kampu, o b ir c - simetrijos įstrižainių atžvilgiu. Tada veiksmų lentelė šioje grupėje

. e a b c

e e a b c

a a e c b

b b c e a

c c b a e

ir Le = = id, La = = (ea)(bc), Lb = = (eb)(ac),
Lc = = (ec)(ab).

Pavyzdys 2

Ciklinės grupės ( pvz. n-tojo laipsnio šaknų iš 1 multiplikacinės grupės) įdėjimas į simetrinę grupę.

Tegu e - primityvioji n-tojo laipsnio ðaknis ið vieneto. Tada visos n-tojo laipsnio ðaknys ið vieneto yra primityviosios ðaknies e laipsniai: e, e2, ..., en-1, en = 1 ir

Le =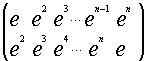

Le2 =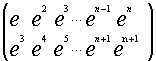

ir t.t Pavyzdžiui, kai n=6, turime reiškimą keitiniais:

L1 = = (123456)

L2 = = (135)(246)

L3 = = (14)(25)(36)

L4 = = (153)(264)

L5 = = (165432)

L6 = = id.