RIMANTAS GRIGUTIS

 

Paskaitų ciklas apie kūnus

Išankstinės žinios

 

GRUPĖS

Liekanų klasių adicinė grupė Zn;

Primityviųjų klasių multiplikacinė grupė Um, |Um| = φ(m)

Vieneto šaknų multiplikacinė grupė U(n).

Apibrėžimas:

Grupės A pogrupis vadinamas normaliuoju, jeigu visiems a Ī A: a × B = B × a.

Normaliojo pogrupio požymis:

a × B × a-1 Ķ B.

Svarbiausia normaliųjų pogrupių savybė yra ta, kad grupės A sluoksnių normaliojo pogrupio B atžvilgiu aibėje (žymuo A/B) galima apibrėžti grupės struktūrą.

Be to, bet kurio grupių homomorfizmo branduolys yra normalusis pogrupis ir bet kuris normalusis pogrupis yra homomorfizmo branduolys.

Teorema (homomorfizmų teorema grupėms):

Tegu f : A (r) B yra grupių homomorfizmas. Tada egzistuoja vienintelis homomorfizmas : A/ker f ® B , kurio dėka diagrama

 

 

 

 

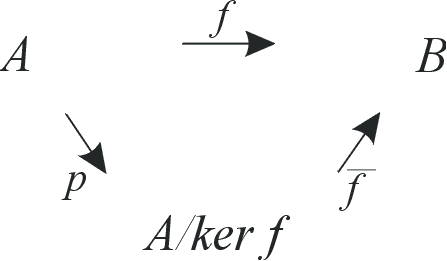
yra komutatyvi, t.y. f = × p, yra grupių A/ker f ir f (A) izomorfizmas, o p - siurjektyvusis homomorfizmas.

Funkcijos j n : Zn (r) <an>, jn(k1)=ak ir j0 : Z (r) <a>, j0(k)=ak yra izomorfizmai.

Dar vienas izomorfizmas Sn/An » C2.

Apibrėžimas:

Tegu p ir r - keitiniai aibėje V. Keitinių sandauga s = p o r vadinsime keitinį, apibrėžtą lygybe s (vi)=r (p (vi)), " vIĪV.

Pastebėsime, kad taip apibrėžta sandauga yra funkcijų kompozicija. Ji nėra komutatyvi.

Pavyzdys:

Kai p =, o r = , tai p o r = ¹ = r o p .

Tačiau, keitinio p kanoniniame skaidinyje esantys nepriklausomi ciklai komutuoja poromis.

Teiginys:

Tegu S(V) - visų keitinių aibė aibėje V . Tada (S(V), o ) - grupė.

Teorema(A.Cayley):

Tegu (G, × ) yra baigtinė grupė, turinti n elementų. Tada egzistuoja funkcija
f : G (r) S(G) =Sn, tenkinanti savybes:

f(g1)=f(g2) Ū g1=g2 (injektyvumas),

f(g× h)=f(g) × f(h) (homomorfizmas).

Įrodymas.

" aĪG konstruojame keitinį La : G (r) G , La(g) =g × a . Taigi La Ī Sn.

Turime aibių lygybę

{g1, g2, ..., gn} = {g1×a, g2×a, ..., gn×a} = G.

Turime

1) LaĪ Sn;

2) (La)-1 = La-1

3) La× b(g) = g × (a × b) = (g × a) × b = Lb(La(g)) = (La o Lb)(g), taigi La× b = La o Lb.

Gavome, kad keitiniai Lg1, Lg2, ..., Lgn sudaro grupę H Ģ S(G) = Sn.

Funkcija f : G (r) H Ģ Sn apibrėžta formule f(g) =Lg.

Įrodyta.

Pavyzdys 1

Rombo simetrijų grupės įdėjimas į simetrinę grupę.

Tegu G = {e, a, b, c} - rombo simetrijų grupė. Čia e ir a posūkiai atitinkamai 0° ir 180° kampu, o b ir c - simetrijos įstrižainių atžvilgiu. Tada veiksmų lentelė šioje grupėje

. e a b c

e e a b c

a a e c b

b b c e a

c c b a e

ir Le==id, La==(ea)(bc), Lb==(eb)(ac), Lb==(ec)(ab).

Pavyzdys 2

Ciklinės grupės ( pvz. n-tojo laipsnio šaknų iš 1 multiplikacinės grupės) įdėjimas į simetrinę grupę. Tegu e - primityvioji n-tojo laipsnio šaknis iš vieneto. Tada visos n-tojo laipsnio šaknys iš vieneto yra primityviosios šaknies e laipsniai: e, e2, ..., en-1, en = 1 ir

Le =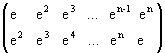

Le2 =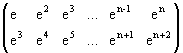

ir t.t Pavyzdžiui, kai n=6, turime reiškimą keitiniais:

L1 = = (123456)

L2 = = (135)(246)

L3 = = (14)(25)(36)

L4 = = (153)(264)

L5 = = (165432)

L6 = = id.

 

ŽIEDAI

Teorema (homomorfizmų teorema žiedams):

Jeigu j : R ® S yra žiedo R homomorfizmas ant žiedo S, tai Ker j - idealas ir
S » R/Ker j .

Jeigu J Ģ R yra idealas, tai f : R ® R/J, j (a) =a + J yra žiedų homomorfizmas, kurio branduolys Ker j = J.

Teorema:

Tegu f (x) Ī K [x]. Faktoržiedis K[x]/(f) yra kūnas tada ir tik tada, kai f - neredukuojamas virš kūno K polinomas.

 

KŪNAI

 

Apibrėžimas:

Tegu K - kūnas. Trupmenų aibėje {|f(x), g(x)Ī K[x], g(x)¹ 0}, kurioje Ū f1g2=f2g1 (tai ekvivalentumo sąryšis), apibrėžus dvi operacijas:
= ir =, gauname racionaliųjų skaičių kūną K(x).

 

VEKTORINĖS ERDVĖS

Teorema apie izomorfizmą:

Tegu A : U ® V - tiesinis atvaizdis. Poerdvis im A izomorfinis faktorerdvei U/ker A.

Įrodymas.

Apibrėžkime funkciją i : U/ker A ® imA formule i(ū) = A(u).

Parodysime, kad tai ir yra ieðkomas izomorfizmas.

Funkcija i yra tiesinis atvaizdis:

I(a1ū1+a2ū2) = I() = A(a1u1+a2u2) = a1A(u1) + a2A(u2) = a1i(ū1) + a2i(ū2).

Tiesinis atvaizdis i yra monomorfizmas:

i (ū) =0 - A(u) = 0 - u Ī ker A - ū = .

Tiesinis atvaizdis i yra epimorfizmas:

su kiekvienu v Ī imA egzistuoja u Ī U, kad A(u) = v, t.y. i (ū) = A(u) = v.

Įrodyta.

Teorema apie izomorfizmą dažnai reškiama tokia komutatyvia diagrama:


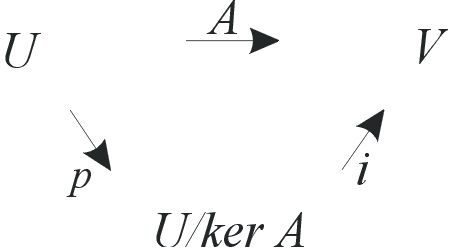
čia p(u) = ū; i(ū) = A(u), taigi, A(u) = i(p(u)).

Pastaba:

Paskutiniųjų teoremų dėka matome, kaip galėtume mąstyti faktorerdvę. Kiekvienam vektorinės erdvės poerdviui galime apibrėžti tiesinį atvaizdį, kurio vaizdas yra šis poerdvis, o branduolys - poerdvio tiesioginis papildinys. Pagal teoremą apie izomorfizmą faktorerdvėje galime mąstyti kaip poerdvio tiesioginį papildinį.

Teorema:

Vektorinė erdvė U, k, dimU = n; yra izomorfinė aritmetinei erdvei kn.

Įrodymas.

Tegu vektorių sistema v1, …, vn - vektorinės erdvės U bazė.

Apibrėžkime tiesinį atvaizdį : kn ® U formule

A = (v1, …, vn) .

imA = U; nes sistema v1, …, vn - generuojanti erdvę U sistema.

ker A = 0; nes sistema v1, …, vn - tiesiðkai nepriklausoma sistema.

Gavome, kad U yra izomorfinė aritmetinei erdvei kn.

Įrodyta.

Pastaba:

U » kn, bet šis izomorfizmas nėra kanoninis - jis priklauso nuo bazių.

Paskutinioji teorema rodo, kad baigtinės dimensijos vektorinę erdvę galima reikšti aritmetinės erdvės elementais, t.y. stulpeliais:

a1u1 + … + anun ® .