VII
KOMANDINĖ KALĖDINĖ RASEINIŲ KRAŠTO OLIMPIADA
PROFESORIAUS JONO KUBILIIAUS TAUREI
LAIMĖTI
Raseiniai , 2006-12-12
1. Mažiausias skaičius, kurį dviem skirtingais būdais galima užrašyti 3
skirtingų sveikų teigiamų daugiklių sandauga taip, kad visi 6 daugikliai būtų
skirtingi, yra
|
(A) 24 |
(B) 32 |
(C) 36 |
(D) 48 |
(E) 60 |
2. Kiek sprendinių turi angliška žodžių lygybė SEVEN + ONE = EIGHT? Čia, kaip įprasta, kiekviena raidė reiškia vieną kurį skaitmenį nuo 0 iki 9, skirtingas raides atitinka skirtingi, o vienodas raides atitinka vienodi skaitmenys, ir joks skaičius neprasideda 0.
|
(A) 0 |
(B) 1 |
(C) 3 |
(D) 7 |
(E) 8 |
3. Realieji skaičiai x, y ir z
yra visi skirtingi ir tenkina sąlygas
x² - x - y = y² - y z = z² - z - x. Raskite
sandaugą (x + y)(y + z)(z + x).
|
(A) -1 |
(B) 0 |
(C) 1 |
(D)
2006 |
(E) nustatyti neįmanoma |
4. AK ir BM yra trikampio ABC pusiaukampinės. Raskite
mažiausiąjį to trikampio kampą, jeigu yra žinoma, kad AK = BM = AB.
|
(A)
15º |
(B) 18º
|
(C) 30º |
(D) 36º
|
(E) 40º |
5. Šachmatų turnyre dalyvavo 20
žaidėjų. Kiekvienas žaidėjas su kiekvienu kitu žaidėju sužaidė po vieną
partiją. Žaidžiant šachmatais už laimėtą partiją skiriamas 1 taškas, už
lygiąsias skiriama ½ taško, o už pralaimėtą partiją žaidėjas gauna 0 taškų.
Suvedus rezultatus paaiškėjo, kad visi dalyviai surinko po skirtingą taškų
skaičių. Kiek mažiausiai taškų galėjo būti surinkęs turnyro nugalėtojas?
|
(A) 16 |
(B)
15,5 |
(C) 15 |
(D)
14,5 |
(E) 14 |
6. Lygčių sistemą
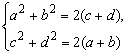
spręskime sveikaisiais neneigiamais skaičiais a, b, c ir d . Kiek sprendinių turi ši lygtis?
|
(A) 0 |
(B) 1 |
(C) 2 |
(D) 3 |
(E) ne mažiau negu 4 |
7. Magdė užrašė skaičių, pamatė, kad
jis dalijasi iš savo paskutiniojo skaitmens ir padalijo tą skaičių iš jo.
Pasirodė, kad gautasis skaičius vėl dalijasi iš savo paskutiniojo skaitmens ir
Magdė vėl tą gautąjį skaičių padalijo iš jo ir t.t. Po 10 dalijimų Magdė gavo 1, be to, visi prieš tai
atlikti dalijimo rezultatai buvo didesni už 1. Kiek yra tokių skaičių?
|
(A) 3 |
(B) 7 |
(C) 8 |
(D) 9 |
(E) daugiau
negu 10 |
8. Lygties (1/101+1/204+1/309+
+1/1100)·X =
(1/11+1/24+1/39+
+1/11000) sprendinys X yra
|
(A) 1 |
(B) 10 |
(C)
10,9 |
(D) 11 |
(E) 11,1 |
9. Raseinių Žemaičio gimnazijos moksleivių Taryboje yra 14 žmonių.
Taryboje yra sudarytos komisijos atskirų dalykų dėstymui remti. Jokioje
komisijoje negali būti mažiau kaip 3 nariai ir jokios dvi komisijos negali būti
sudarytos iš vienų ir tų pačių narių. Kiekviena komisija iš savo narių
išsirenka pirmininką. Nė vienas Tarybos narys negali priklausyti daugiau negu 2
komisijoms, ir kiekvienas komisijos pirmininkas negali įeiti į jokią kitą
komisiją nei nariu, nei pirmininku. Kiek
daugiausiai komisijų gali būti sudaryta
Raseinių Žemaičio gimnazijos moksleivių Taryboje?
|
(A) 3 |
(B) 4 |
(C) 5 |
(D) 6 |
(E) 7 |
10. Kiek yra 10-ženklių skaičių, kurių visi
skaitmenys yra skirtingi ir kurie dalijasi be liekanos iš 11 111?
|
(A) 123 |
(B) 234 |
(C)
1111 |
(D)
3456 |
(E) 6790 |