There are two ways to describe the sensitivity of a camera. First, we can determine the minimum number of detectable photoelectrons. This can be termed the absolute sensitivity. Second, we can describe the number of photoelectrons necessary to change from one digital brightness level to the next, that is, to change one analog-to-digital unit (ADU). This can be termed the relative sensitivity.
of, say, 100
photoelectrons, then to ensure detectability of a signal we could then say
that, at the 3 level, the minimum detectable signal (or
absolute sensitivity) would be 300 photoelectrons. If all the noise sources
listed in Section 6, with the exception of photon noise, can be reduced to
negligible levels, this means that an absolute sensitivity of less than 10
photoelectrons is achievable with modern technology
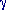= 1, leads immediately to the
result:
The measurement of the sensitivity or gain can be performed in two distinct ways.
* If, following eq. , the input signal a can be precisely controlled
by either "shutter" time or intensity (through neutral density filters), then
the gain can be estimated by estimating the slope of the resulting
straight-line curve. To translate this into the desired units, however, a
standard source must be used that emits a known number of photons onto the
camera sensor and the quantum efficiency (
) of the sensor must be
known. The quantum efficiency refers to how many photoelectrons are
produced--on the average--per photon at a given wavelength. In general 0 <=
(
) <= 1.
* If, however, the limiting effect of the camera is only the photon (Poisson) noise (see Section 6.1), then an easy-to-implement, alternative technique is available to determine the sensitivity. Using equations , , and and after compensating for the offset (see Section 10.1), the sensitivity measured from an image c is given by:
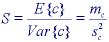
where mc and sc are defined in equations and .
Measured data for five modern (1995) CCD camera configurations are given in Table 9.
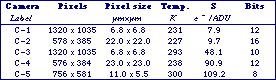
Table 9: Sensitivity measurements. Note that a more sensitive camera has a lower value of S.
The extraordinary sensitivity of modern CCD cameras is clear from these data. In a scientific-grade CCD camera (C-1), only 8 photoelectrons (approximately 16 photons) separate two gray levels in the digital representation of the image. For a considerably less expensive video camera (C-5), only about 256 photoelectrons (approximately 512 photons) separate two gray levels.