Image Processing Fundamentals - Sampling Density for Image Analysis

Sampling Density for Image Analysis

Sampling for area measurements
Sampling for length measurements
Conclusions on sampling

The "rules" for choosing the sampling density when the goal is image analysis--as opposed to image processing--are different. The fundamental difference is that the digitization of objects in an image into a collection of pixels introduces a form of spatial quantization noise that is not bandlimited. This leads to the following results for the choice of sampling density when one is interested in the measurement of area and (perimeter) length.

Sampling for area measurements

Assuming square sampling, X_o = Y_o and the unbiased algorithm for estimating area which involves simple pixel counting, the CV (see eq. ) of the area measurement is related to the sampling density by :

and in D dimensions:

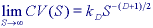
where S is the number of samples per object diameter. In 2D the measurement is area, in 3D volume, and in D-dimensions hypervolume.

Sampling for length measurements

Again assuming square sampling and algorithms for estimating length based upon the Freeman chain-code representation (see Section 3.6.1), the CV of the length measurement is related to the sampling density per unit length as shown in Figure 17 (see .)

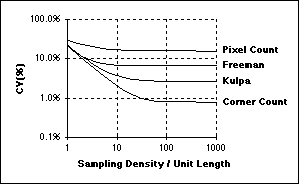
Figure 17: CV of length measurement for various algorithms.

The curves in Figure 17 were developed in the context of straight lines but similar results have been found for curves and closed contours. The specific formulas for length estimation use a chain code representation of a line and are based upon a linear combination of three numbers:

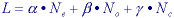
where N_e is the number of even chain codes, N_o the number of odd chain codes, and N_c the number of corners. The specific formulas are given in Table 7.

Coefficients	`a`
Formula				Reference
Pixel count	1	1	0	[18]
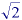
Freeman	1		0	[11]
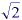
Kulpa	0.9481	0.9481 *	0	[20]
Corner count	0.980	1.406	-0.091	[21]

Table 7: Length estimation formulas based on chain code counts (N_e, N_o, N_c)

Conclusions on sampling

If one is interested in image processing, one should choose a sampling density based upon classical signal theory, that is, the Nyquist sampling theory. If one is interested in image analysis, one should choose a sampling density based upon the desired measurement accuracy (bias) and precision (CV). In a case of uncertainty, one should choose the higher of the two sampling densities (frequencies).